Came across this very informative website https://astro.ucla.edu/~wright/cosmo_02.htm , and it has the following two diagrams. I'm having trouble figuring out why "But the Hubble law distance $D_{now}$, which is measured now, of these most distant galaxies is infinity (in this model)." (highlighted in the screenshot). Which particular point or line in which of the two diagram indicates that the "now" distance is $\bf {infinite}$? It'd be great if someone could point out what I'm missing. Thank you.
The time and distance used in the Hubble law are not the same as the $x$ and $t$ used in special relativity, and this often leads to confusion. In particular, galaxies that are far enough away from us necessarily have velocities greater than the speed of light:
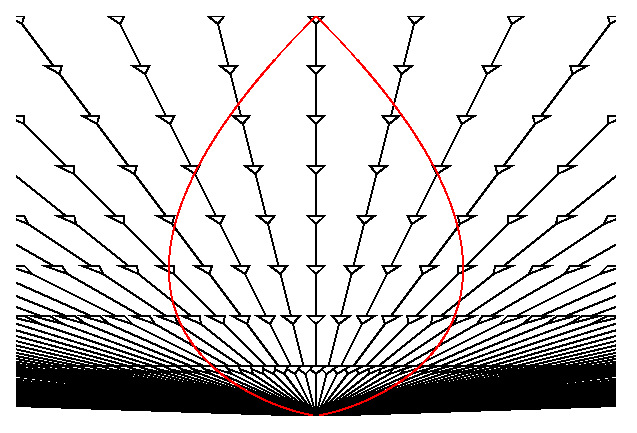
The light cones for distant galaxies in the diagram above are tipped over past the vertical, indicating $v > c$. The space-time diagram below shows a "zero" (really very low) density cosmological model plotted using the $D_\text{now}$ and $t$ of the Hubble law.
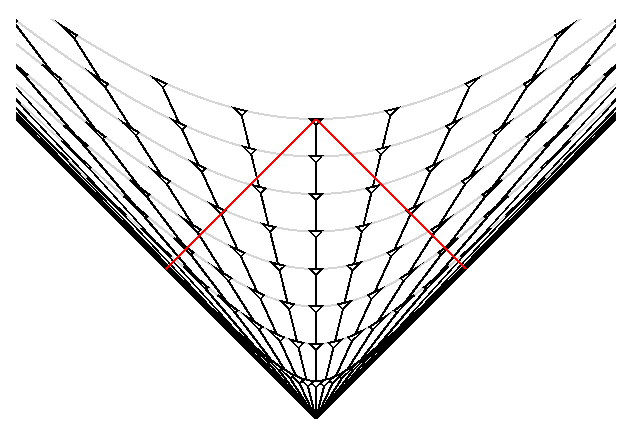
Worldlines of comoving observers are plotted and decorated with small, schematic lightcones. The red pear-shaped object is our past light cone. Notice that the red curve always has the same slope as the little light cones. In these variables, velocities greater than $c$ are certainly possible, and since the open Universes are spatially infinite, they are actually required. But there is no contradiction with the special relativistic principle that objects do not travel faster than the speed of light, because if we plot exactly the same space-time in the special relativistic $x$ and $t$ coordinates we get:
The grey hyperbolae show the surfaces of constant proper time since the Big Bang. When we flatten these out to make the previous space-time diagram, the worldlines of the galaxies get flatter and giving velocities $v = dD_\text{now}/dt$ that are greater than $c$. But in special relativistic coordinates the velocities are less than $c$. We also see that our past light cone crosses the worldline of the most distant galaxies at a special relativistic distance $x = c\cdot t_o/2$. But the Hubble law distance $D_\text{now}$, which is measured now, of these most distant galaxies is infinity (in this model). Furthermore, this galaxy with infinite Hubble law distance and hence infinite Hubble law velocity is visible to us, since in this model the observable Universe is the entire Universe. The relationships between the Hubble law distance and velocity ($D_\text{now}$ & $v$) and the redshift $z$ for the zero density model are given below:
(boldface added)

Best Answer
Horizontal lines in the upper figure, gray hyperbolas in the lower figure, are "spatial" surfaces in this model. Focusing on the lower figure, the uppermost hyperbola is the "present time" spatial surface. Note that its total length is infinite ("space is infinite").
The black lines are worldlines of comoving objects like galaxies. Since space is infinite, there are of course infinitely many of them. In the lower figure they appear to get bunched together at large distances, but that's just an artifact of drawing Minkowski geometry on a Euclidean computer screen. All of these lines are in fact equally separated along the aforementioned spatial surfaces. If you were to draw the same diagram from the point of view of any other galaxy, it would look the same.
Now, if you trace a light ray (red line) backward, it crosses the worldline of every galaxy, even galaxies that are arbitrarily far "at the present time" (along the uppermost hyperbola). That's what "$D_\mathrm{now}$ is infinite" means.