Using the reflection formula followed by the recurrence formula and the Beta integral representation (DLMF)
\begin{align}
\frac{x(1-x)}{\sin \pi x}&=\frac{1}{\pi}x(1-x)\Gamma(x)\Gamma(1-x)\\
&=\frac{1}{\pi}\Gamma(x+1)\Gamma(2-x)\\
&=\frac{2}{\pi}B(1+x,2-x)\\
&=\frac{2}{\pi}\int_0^\infty \frac{t^x}{(1+t)^3}\,dt\\
&=\frac{1}{2\pi}\int_{-\infty}^{\infty}\frac{e^{u(2x-1)}}{\cosh^3u}\,du
\end{align}
last expression is obtained with $t=e^{2u}$. Then, for calculating
\begin{equation}
I_f=\int_0^1\frac{x(1-x)}{\sin \pi x}f(x)\,dx
\end{equation}
one can express
\begin{align}
I_f&=\frac{1}{2\pi}\int_0^1\int_{-\infty}^{\infty}\frac{e^{u(2x-1)}}{\cosh^3u}\,duf(x)\,dx\\
&=\frac{1}{2\pi}\int_{-\infty}^{\infty}\frac{e^{-u}}{\cosh^3u}\,du\int_0^1e^{2ux}f(x)\,dx\\
&=\frac{1}{2\pi}\int_{-\infty}^{\infty}\frac{e^{-u}}{\cosh^3u}F(u)\,du \label{eq:intf}
\end{align}
assuming that the change of the integration order is valid and denoting
\begin{equation}
F(u)=\int_0^1e^{2ux}f(x)\,dx
\end{equation}
If $F(u)$ is analytic in the half-plane $\Im(u)>0$ and $\left|F(u)\right|=o\left(\frac{e^{4u}}{u} \right)$ for $\left|u\right|\to \infty$,$I_f$ is evaluated by integrating along the real axis closed by the semi-large circle $\Im(u)>0$, using the residue method. Poles are situated at $u_n=i(2n+1)\pi/2$ with $n=0,1,2...$. Residues are $1/2F''(i(2n+1)\pi/2)-F'(i(2n+1)\pi/2)$, where $F''(z)$ and $F'(z)$ are respectively the first and second derivative of $F(z)$. As the half-circle contribution vanishes, it comes
\begin{equation}
I_f=i\sum_{n=0}^\infty\left[\frac{1}{2}F''(i(2n+1)\frac{\pi}{2})-F'(i(2n+1)\frac{\pi}{2})\right]
\end{equation}
When $f(x)=1$, to express the original integral, $F(u)=\frac{e^{2u}-1}{2u}$, a simple calculation shows, as expected, that
\begin{equation}
I=\frac{8}{\pi^3}\sum_{n=0}^\infty \frac{1}{(2n+1)^3}=\frac{7\zeta(3)}{\pi^3}
\end{equation}
Another expression for the result is obtained by derivation under the integral
\begin{equation}
I_f=-2i\sum_{n=0}^\infty \int_0^1x(1-x)f(x)e^{i(2n+1)\pi x}\,dx
\end{equation}
For a real function $f$, as the summation should be real, it is sufficient to keep the imaginary contribution to the integral:
\begin{equation}
I_f=2\sum_{n=0}^\infty \int_0^1x(1-x)f(x)\sin\left( (2n+1)\pi x \right)\,dx
\end{equation}
Now, suppose that a function $f_p$ is known such that the integrals
\begin{equation}
J_p=\int_0^1x(1-x)f_p(x)\sin\left( (2n+1)\pi x \right)\,dx=\frac{A_p}{(2n+1)^{2p+1}}
\end{equation}
which gives the relation
\begin{equation}
I_{f_p}=2A_p\sum_{n=0}^\infty\frac{1}{(2n+1)^{2p+1}}=2A_p\left( 1-2^{-2p-1} \right)\zeta(2p+1)
\end{equation}
Denoting the function $Q^0(x)=x(1-x)f_p(x)$ and $Q^1,Q^2(x)$ its first and second antiderivative. Two successive integrations by parts can be performed:
\begin{align}
J_p&=-(2n+1)\pi \int_0^1Q^1(x)\cos\left( (2n+1)\pi x \right)\,dx\\
&=(2n+1)\pi\left[Q^2(1)+Q^2(0)\right]-(2n+1)^2\pi^2\int_0^1Q^2(x)\sin\left( (2n+1)\pi x \right)\,dx \label{eq:jp}
\end{align}
The free parameters in $Q^2(x)$ can be chosen in order that $Q^2(1)=Q^2(0)=0$. With
\begin{equation}
Q^2(z)=\int_0^zdt\int_0^tQ^0(u)\,du+az+b
\end{equation}
one may chose $b=0$ and $a=-\int_0^1\,dt\int_0^tQ^0(u)\,du$. Thus
\begin{equation}
Q^2(z)=\int_0^zdt\int_0^tQ^0(u)\,du-z\int_0^1\,dt\int_0^tQ^0(u)\,du
\end{equation}
If $f_p(x)$ is a polynomial, then $Q^2(x)$ also. By construction, $x=0$ and $x=1$ are among its roots. It can be written as
\begin{equation}
Q^2(x)=x(1-x)f_{p+1}(x)
\end{equation}
or
\begin{equation}
f_{p+1}(x)=\frac{\int_0^xdt\int_0^tu(1-u)f_p(u)\,du-x\int_0^1\,dt\int_0^tu(1-u)f_p(u)\,du}{x(1-x)}
\end{equation}
$J_p$ can be written as
\begin{equation}
J_p=-(2n+1)^2\pi^2\int_0^1x(1-x)f_{p+1}(x)\sin\left( (2n+1)\pi x \right)\,dx
\end{equation}
One obtain
\begin{equation}
\int_0^1x(1-x)f_{p+1}(x)\sin\left( (2n+1)\pi x \right)\,dx=-\frac{1}{\pi^2}\frac{A_p}{(2n+1)^{2p+3}}
\end{equation}
and thus
\begin{equation}
I_{f_{p+1}}=2A_{p+1}\left( 1-2^{-2p-3} \right)\zeta(2p+3)
\end{equation}
with
\begin{equation}
A_{p+1}=-\frac{A_p}{\pi^2}
\end{equation}
Starting from $f_1(x)=1$ one obtains
\begin{align}
f_2(x)&=\frac{1}{12}(x^2-x-1)\\
f_3(x)&=\frac{1}{360}(x^4-2x^3-2x^2+3x+3)\\
f_4(x)&=\frac{1}{20160}(x^6-3x^5-3x^4+11x^3+11x^2-17x-17)\\
...
\end{align}
which gives
\begin{align}
\int_0^1\frac{x(1-x)}{\sin\pi x}f_2(x)\,dx&=-\frac{31}{4}\frac{\zeta(5)}{\pi^5}\\
\int_0^1\frac{x(1-x)}{\sin\pi x}f_3(x)\,dx&=\frac{127}{16}\frac{\zeta(7)}{\pi^7}\\
\int_0^1\frac{x(1-x)}{\sin\pi x}f_4(x)\,dx&=-\frac{511}{64}\frac{\zeta(9)}{\pi^9}\\
...
\end{align}
Starting from $f_1(x)=x(3-x)$, other series can be obtained. For example
\begin{align}
&f_2(x)=\frac{1}{60}(2x^4-10x^3+5x^2+5x+5)\\
&f_3(x)=-\frac{1}{5040}(3x^6-21x^2(x^3-x^2-x-1)-49(x+1))\\
&\int_0^1\frac{x(1-x)}{\sin\pi x}f_2(x)\,dx=-\frac{381}{4}\frac{\zeta(7)}{\pi^7}\\
&\int_0^1\frac{x(1-x)}{\sin\pi x}f_3(x)\,dx=-\frac{1533}{16}\frac{\zeta(9)}{\pi^9}
\end{align}
Other starting points can be obtained by choosing other members of the list proposed in the question above. For example, starting from $f_1(x)=x^2P_3(x)$ above leads to an apparent different expression for $\zeta(9)$:
\begin{align}
&f_2(x)=-\frac{1}{56}(x^6-27x^5+57x^4-13x^3-13x^2-13x-13)\\
&\int_0^1\frac{x(1-x)}{\sin\pi x}f_2(x)\,dx=-\frac{22995}{8}\frac{\zeta(9)}{\pi^9}
\end{align}
Obtained polynomials are not of the form $x^pP_p(x)$ as discussed in the question, however the above method may perhaps be adapted in this case.
EDIT 04/06/2017 : (sorry for the length of this answer...)
One may characterize more precisely the family of these polynomials.
It helps to symmetrize the expressions:
\begin{equation}
I_f=\int_0^1\frac{x(1-x)}{\sin \pi x}f(x)\,dx=\frac{1}{8}\int_{-1}^1\frac{1-y^2}{\cos\pi y/2}g(y)\,dy
\end{equation}
with $g(y)=f(x)$ and $x=(1+y)/2$. In this form it is clear that odd contribution of the polynomial $g(y)$ vanishes. The same symmetrization for the proposed decomposition above reads:
\begin{equation}
I_f=\frac{(-1)^n}{4}\sum_{n=0}^\infty \int_{-1}^1(1-y^2)g(y)\cos\left( (2n+1) \frac{\pi y}{2} \right)\,dy
\end{equation}
One may adapt the method developed above. If $g_p(y)$ is an even polynomial such as
\begin{equation}
\sum_{n=0}^\infty \int_{-1}^1(1-y^2)g_p(y)\cos\left( (2n+1) \frac{\pi y}{2} \right)\,dy=\frac{A_p}{(2n+1)^{2p+3}}
\end{equation}
then, by integrating twice by part, the polynomial
\begin{equation}
g_{p+1}(y)=\frac{\int_{-1}^ydt\int_{-1}^t(1-u^2)g_p(u)\,du-\frac{y+1}{2}\int_{-1}^1\,dt\int_{-1}^t(1-u^2)g_p(u)\,du}{1-y^2}
\end{equation}
is such that
\begin{equation}
\sum_{n=0}^\infty \int_{-1}^1(1-y^2)g_{p+1}(y)\cos\left( (2n+1)\frac{\pi y}{2} \right)\,dy=\frac{A_{p+1}}{(2n+1)^{2p+5}}
\end{equation}
with $A_{p+1}=-4A_p/\pi^2$.
thus
\begin{equation}
\frac{1}{8}\int_{-1}^1\frac{1-y^2}{\cos\pi y/2}g_{p+1}(y)\,dy=2A_{p+1}\left( 1-2^{-2p-3} \right)\zeta(2p+5)
\end{equation}
One may show that $g(y)$ is an even polynomial of $y$. For $g_0(y)=1$ one has, as expected
\begin{equation}
\frac{1}{8}\int_{-1}^1\frac{1-y^2}{\cos\pi y/2}\,dy= \frac{7\zeta(3)}{\pi^3}
\end{equation}
Then, the recurrence above produces a series of even polynomials $g_p(y)$ of degree $2p$ giving successive integral expressions for $\zeta(2p+3)$. Due to the parity remark, one can conclude that any polynomial $Q(y)$, with its even power coefficient identical to that of $g_p(y)$, is such that
\begin{equation}
\int_{-1}^1\frac{1-y^2}{\cos\pi y/2}Q(y)\,dy=\left( -1 \right)^p8\left( 2^{2p+3}-1 \right)\frac{\zeta(2p+3)}{\pi^{2p+3}}
\end{equation}
The condition reads
\begin{equation}
Q(y)+Q(-y)=2g_p(y)
\end{equation}
The first polynomials (written with $Y=y^2$) are:
\begin{align}
g_0(y)&=1\\
g_1(y)&=\frac{1}{12}\left( Y-5 \right)\\
g_2(y)&=\frac{1}{360}\left( Y^2-14Y+61 \right)\\
g_3(y)&=\frac{1}{20160}\left( Y^3-27Y^2+323Y-1385 \right)\\
g_4(y)&=\frac{1}{1814400}\left( Y^4-44Y^3+1006Y^2-11804Y+50521 \right)\\
g_5(y)&=\frac{1}{239500800}\left( Y^{5}-65Y^4+2410Y^3-53954Y^2+631621Y-2702765\right)\\
g_6(y)&=\frac{1}{43589145600}\left(Y^6-90Y^5+4915Y^4-178268Y^3+3980887Y^2-46590634Y+199360981 \right)
\end{align}
In terms of the non-symmetrized function, any polynomial of the form
\begin{equation}
f(x)=g_p\left( 2x-1 \right)+P(2x-1)
\end{equation}
where $P(z)$ is an arbitrary odd polynomial, gives a result proportional to $\zeta(2p+1)$ when integrated as in $I_f$ defined above.

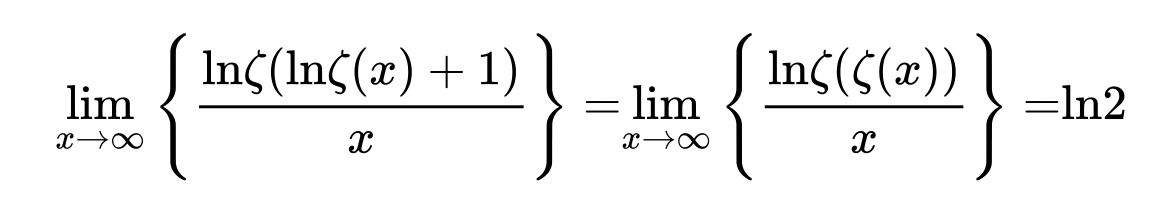
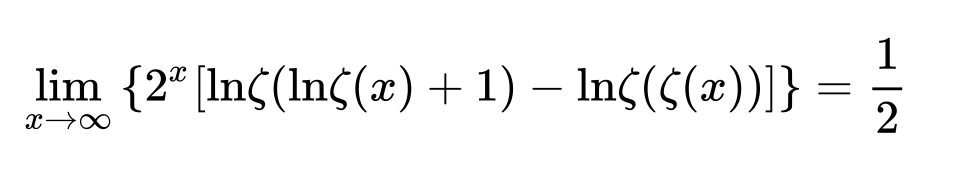
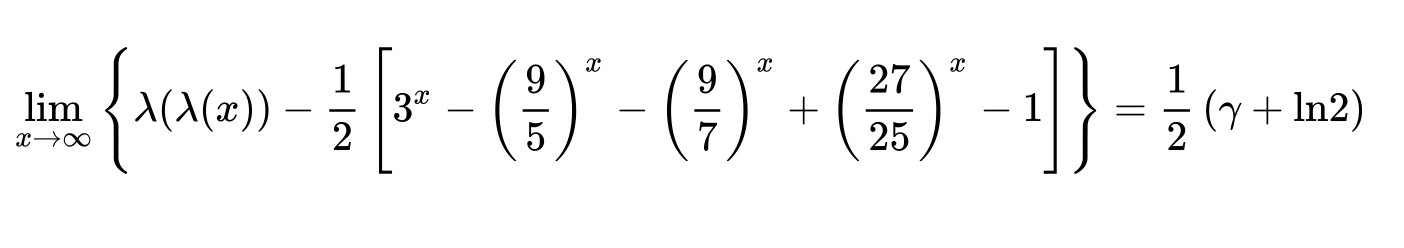
Best Answer
For $n\geq 1$ and $m\geq 0$, an application of integration by parts ($u=\log^n(1-x)$, $dv=\log^m(x)\,dx/x$) followed by the substitution $x\mapsto 1-x$ shows that $$ \frac{I_{n,m}}{I_{m+1,n-1}}=\frac{n}{m+1}. $$ All of your examples are special cases of this identity.