[Math] Tying knots with reflecting lightrays

gt.geometric-topologyknot-theorymg.metric-geometry

Let a lightray bounce around inside a cube whose faces
are (internal) mirrors.
If its slopes are rational, it will eventually form a cycle.
For example, starting with a point $p_0$ in the interior
of the $-Y$ face of an axis-aligned cube, and initially heading in a direction
$v_0=(1,1,1)$, the ray will rejoin $p_0$ after 5 reflections,
forming a hexagon.
The figure below shows a more complicated 16-cycle.

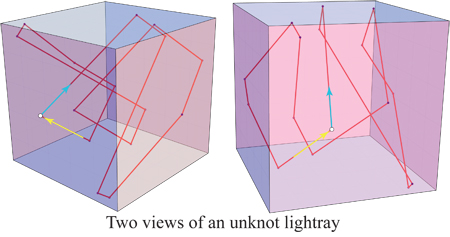
16-cycle of rays

Assume that $p_0$ and $v_0$ are chosen so that
(a) the ray never directly hits an edge or corner of the cube,
and (b) the ray path never self-intersects inside the cube.

Can every knot type be realized by a lightray reflecting inside in a cube?

The figure above is an unknot.
I believe (but am not certain) the 31-cycle below is knotted:

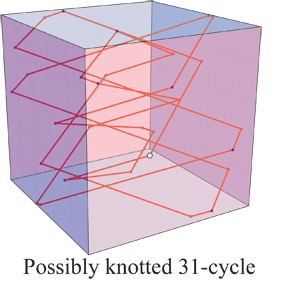
          Knotted 31-cycle

Any such knotted path is a stick representation of the knot,
but perhaps the many unsolved problems in stick representations
are not relevant to this situation.
My question is related to the probability of random knots
forming under various models, but usually those models are
aimed at polymers or DNA. I have not seen this lightray model
explored, but would be interested to know of related models.

The choice of $(p_0,v_0)$ allows considerable freedom to "design"
a knot, but it seems difficult to control the structure of the path
to achieve a particular result.
I've explored tiling space by reflected cubes so
that the lightray may be viewed as a straight segment between
two images of $p_0$, but this viewpoint is not yielding
me insights.

If anyone has ideas, however partial, I would appreciate hearing them.
Thanks!

Edit1 (15Sep10).
I have not been able to yet access the
Jones-Przytycki paper that Pierre cites, but knowing the
keywords he kindly provided, I did
find related work by
Christoph Lamm
("There are infinitely many Lissajous knots"
Manuscripta Mathematica
93(1): 29-37
(1997))
that provides useful information:

  1. Theorem: Billiard knots in a cube are isotopic to Lissajous knots.

  2. As Pierre said, many knots are unachievable in these models. In particular,
    algebraic knots cannot be achieved.
    The technical result is this.
    Theorem: The Alexander polynomial of a billiard knot is a square
    mod 2.

  3. In 1997, there were several intriguing open problems, including
    these two. (a) Is every knot a billiard knot in some convex polyhedron?
    (b) Can the unknot be achieved in every convex polyhedron that supports periodic paths?

Edit2 (15Sep10). Here is a little more information on open problems ca. 2000,
found in a list by Jozef H. Przytycki in the book that resulted from
Knots in Hellas '98:

  1. Is there a manifold that supports every knot?
    (By "supports every knot" he means there is a billiard path isotopic to every knot type.)

  2. Is there a finite polyhedron that supports every knot?
    There apparently is an "infinite polyhedron" that supports every knot.

  3. More specifically, is there a convex polyhedron that supports every knot? (This is 3(a) above.) [See Bill Thurston's correction below!]

  4. Even more specifically, is every knot supported by one of the Platonic solids?

I have not been successful in finding information on this topic later than 2000.
If anyone knows later status information, I would appreciate a pointer. Thanks for the interest!

Edit3 (5Jul11).
The question has been answered (affirmatively) in a paper by
Pierre-Vincent Koseleff and Daniel Pecker
recently (28Jun11) posted to the arXiv:
"Every knot is a billiard knot":

"We show that every knot can be realized as a billiard trajectory in a convex prism. …
Using a theorem of Manturov [M], we first prove that every knot has a diagram which is a star polygon.
[…Manturov’s theorem tells us that every knot (or link) is realized as the closure of a quasitoric braid…]
Then, perturbing this polygon, we obtain an irregular diagram of the same knot. We deduce that it is possible to suppose that 1 and the arc lengths of the crossing points are linearly independent over $\mathbb{Q}$. Then, it is possible to use the classical Kronecker density theorem to prove our result."

Edit4 (4Oct11).
A new paper was released by Daniel Pecker, "Poncelet's theorem and Billiard knots," arXiv:1110.0415v1. The context is that, earlier, "Lamm and Obermeyer proved that not all knots are billiard knots in a cylinder," and Lamm conjectured an elliptic cylinder would suffice.
Here is the abstract:

Let $D$ be any elliptic right cylinder. We prove that every type of knot can be realized as the trajectory of a ball in $D$. This proves a conjecture of Lamm and gives a new proof of a conjecture of Jones and Przytycki. We use Jacobi's proof of Poncelet's theorem by means of elliptic functions.

Edit5 (13Nov12).
The Pecker paper cited above is now published:
Geometriae Dedicata,
December 2012, Volume 161, Issue 1, pp 323-333.

Best Answer

These knots seem to be called billiard knots in the literature. They coincide with Lissajous knots as shown by Jones and Przytycki in "Lissajous knots and billiard knots", Banach center Publications 42, 145-163 (1998). Lissajous knots are knots admitting a parametrization of the form $(\cos(n_x t + d_x), \cos(n_y t + d_y), \cos(n_z t + d_z))$. There are strong constraints on such knots (see the wikipedia), and for example no torus knot can be Lissajous.

Related Question