What is the expected height of a stack of unit-length bricks, each one
stacked on the previous with a uniformly random shift within $\pm \delta$?
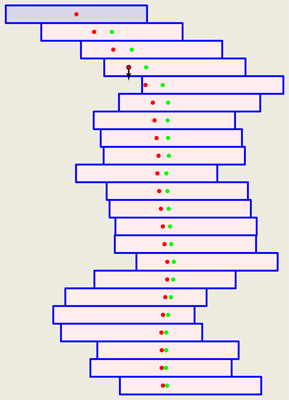
The stack topples if the center of gravity of the top $k$ does
not rest on the brick under that top group. For example,
here I used $\delta = \frac{1}{3}$, and the stack was stable after
the 21st brick was placed (the green top-group center-of-gravity dots),
but the 22nd brick caused the centers of gravity to shift (red dots),
with the cg of the top four bricks (arrow marked) now overhanging
the 18th brick beneath:
Let $N(\delta)$ be the expected height (number of bricks) of such a stack.
Computing this is elementary in some sense,
but I am not arriving at a satisfactory formulation
to let me see the overall growth clearly.
Perhaps this has been studied, given the vast literature
on brick-stack overhangs? If so, a pointer would be appreciated.
I set out to explore random stacks of disks, but even the above simpler
rectangular bricks case is more intricate than I anticipated.

Apologies if all this is too elementary!
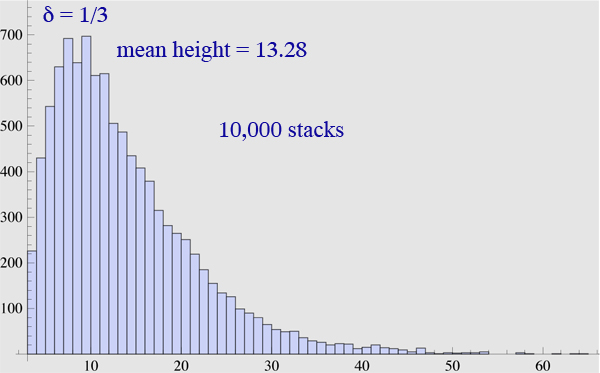
Added. To provide a data point, here is one simulated topple-height histogram:
Update. Here is a plot of Aaron Golden's data, $N(\delta)$ vs. $\delta^{-2}$,
which certainly supports Ori's $\delta^{-2}$ conclusion, as JSE noted:

Best Answer
The distribution should be roughly geometric with expectation roughly $\delta^{-2}$. To bound from above, in every $2\delta^{-2}$ steps there is a constant (independent of $\delta$) probability that the location of the $\delta^{-2}$ brick will be at least offset of 3 from the first brick. Then there is a constant probability for the next $\delta^{-2}$ bricks to be all at offset 2 or more, thus causing collapse. This event can happen independently for every batch of $\delta^{-2}$ bricks, so we get domination by geometric distribution with expectation $O(\delta^{-2})$.
On the other hand, the probability that the center of the brick never strays more than $1/4$ away from the center for $t$ bricks should be roughly $e^{-ct\delta^2}$ so we get bound from below by a geometric distribution with expectation $\Omega(\delta^{-2})$ too.
The coins case should be similar, still $\delta^{-2}$, but with a different constant.