Lets call expansions
$$\langle
x_1,\ldots,x_m\rangle:=\cfrac{1}{x_1-{\atop\ddots\,\displaystyle{-\cfrac{1}{x_m}}}}$$
(as in Perron's book) reduced regular continued fractions (RRCF).
Probably they are older then Hirzebruch.
We'll prove more precise statement.
Theorem. If $(n,ab)=1$ and $n>ab$ then RRCF for all numbers
$$\left\{\frac{ab^{-1}\pmod{(n+kab)}}{n+kab}\right\}\qquad(k\ge
0)$$ are almost equal: they have equal length and differ only in
one partial quotient.
Remark 1. Common factors of $a$ and $b$ can be moved into $k$.
If $d=(a,b)$, $a=da_1$, $b=db_1$, then \begin{gather*} \left\{
\frac{ab^{-1}\pmod{(n+kab)}}{n+kab}\right\} =\left\{
\frac{a_1b_1^{-1}\pmod{(n+kab)}}{n+kab}\right\} \\=\left\{
\frac{a_1b_1^{-1}\pmod{(n+(kd^2)a_1b_1)}}{n+(kd^2)a_1b_1}\right\}.
\end{gather*}
So we can assume that $(a,b)=1$.
Remark 2. The proof will be given in terms of modified
continuants $K(x_1,\ldots, x_n)$ (see ``Concrete Mathematics'' for
more explanations). These polynomials are defined by initial
conditions
$$K()=1,\quad K(x_1)=x_1$$
and the following recurrence:
$$K(x_1,\ldots,
x_n)=x_nK(x_1,\ldots, x_{n-1})-K(x_1,\ldots,
x_{n-2})\qquad(n\ge2).$$ (In the usual definition minus must be
replaced by plus.) For convenience $K_{-1}:=0$ (empty RRCF is
$0$).
In terms of continuants RRCF can be written as
$$\langle x_1,\ldots,x_n\rangle=\frac{K(x_2,\ldots,
x_n)}{K(x_1,\ldots, x_n)}.$$
Continuant's properties. All these properties can be proved by
induction (or from ``Euler’s rule'').
1$^{\circ}.$ $K(x_1,\ldots, x_n)=K(x_n,\ldots, x_{1})$.
2$^{\circ}.$ \begin{gather*} K(x_1,\ldots, x_n,x_{n+1}, \ldots,
x_{m+n})\\=K(x_1,\ldots, x_n)K(x_{n+1}, \ldots,
x_{m+n})-K(x_1,\ldots, x_{n-1})K(x_{n+2}, \ldots, x_{m+n})
\end{gather*}
3$^{\circ}.$ $\begin{vmatrix}
K(x_2,\ldots, x_{n-1})&K(x_2,\ldots, x_n) \\
K(x_1,\ldots, x_{n-1})&K(x_1,\ldots, x_n)
\end{vmatrix}=-1$. In particular if
$$\frac{A}{a}=\left<r_1, \ldots, r_v\right>=\frac{K(r_2, \ldots,
r_v)}{K(r_1, \ldots, r_v)}$$ then
$$K(r_1, \ldots, r_{v-1})=A^{-1}\pmod{a},\qquad K(r_2, \ldots, r_{v-1})=\frac{AA^{-1}\pmod{a}-1}{a}.$$
4$^{\circ}.$ Euler's identity (see A Short Proof of Euler's Identity
for Continuants for additional arguments). (2$^{\circ}$ and
3$^{\circ}$ are special cases of this identity) $$
K(x_1, \ldots, x_{m+n})K(x_{m+1}, \ldots, x_{m+l})-K(x_1, \ldots,
x_{m+l})K(x_{m+1}, \ldots, x_{m+n})$$ $$+K(x_1, \ldots,
x_{m-1})K(x_{m+l+2}, \ldots, x_{m+n})=0.
$$
Proof of the Theorem. For a given $n$ define
$a^{-1}:=a^{-1}\pmod{n}$, $b^{-1}:=b^{-1}\pmod{n}$, $0\le a,b\le n-1$
(inverse number is always least possible nonnegative) and $t_a$,
$t_b$ such that $aa^{-1}=1+t_an$, $bb^{-1}=1+t_bn$. Let $$
\frac{A}{a}=\left\{\frac{bt_a}{a}\right\}=\left<r_1, \ldots,
r_v\right>,\qquad A^{-1}:=A^{-1}\pmod{a};$$
$$\frac{B}{b}=\left\{\frac{at_b}{b}\right\}=\left<q_1, \ldots,
q_u\right>,\qquad B^{-1}:=B^{-1}\pmod{b};$$
$$\frac{P(x)}{Q(x)}=\left<q_1, \ldots, q_u,x,r_v, \ldots,
r_1\right>.
$$
By 2$^{\circ}$, 3$^{\circ}$ and main recurrence $$
Q(x)=K(q_1, \ldots, q_u,x,r_v, \ldots, r_1)=$$
$$xK(q_1, \ldots, q_u)K(r_v, \ldots, r_1)-K(q_1, \ldots,
q_{u-1})K(r_v, \ldots, r_1)-K(q_1, \ldots, q_u)K(r_{v-1}, \ldots,
r_1)$$ $$=xab-aB^{-1}-bA^{-1}.
$$
Hence $$ Q(x)\equiv -bA^{-1}\equiv -b((bt_a)^{-1}\pmod{a})\equiv
-t_a^{-1}\equiv n\pmod{a},$$ $$Q(x)\equiv -aB^{-1}\equiv
-a((at_b)^{-1}\pmod{b})\equiv -t_b^{-1}\equiv n\pmod{b}.$$
Therefore
$$Q(x)\equiv n\pmod{ab},$$
and for some integer $x_0$ we have $Q(x_0)=n$. We know that $n>ab$. It
means that
$$x_0ab-aB^{-1}-bA^{-1}>ab,$$
so $x_0\ge 2$ and $\left<q_1, \ldots, q_u,x_0,r_v, \ldots,
r_1\right>$ is really RRCF. Choosing arbitrary $x=x_0+k$ we'll get
progression $n+kab$ as in the statement of the theorem.
Let's check the numerator $P(x)$. Final step $P(x)\equiv
ab^{-1}\pmod{Q(x)}$ follows from identity
$$bP(x)-BQ(x)=a,$$
which is a special case of Euler's identity. Nevertheless this
identity can be verified directly with help of
1$^{\circ}$--3$^{\circ}$: $$
P(x)=K(q_2, \ldots, q_u,x,r_v, \ldots, r_1)=$$
$$xK(q_2, \ldots, q_u)K(r_v, \ldots, r_1)-K(q_2, \ldots,
q_{u-1})K(r_v, \ldots, r_1)-K(q_2, \ldots, q_u)K(r_{v-1}, \ldots,
r_1)$$ $$=xaB-a\frac{BB^{-1}-1}{b}-BA^{-1},$$ $$
bP(x)-a=B(xab-aB^{-1}-bA^{-1})=BQ(x).
$$
Best Answer
This doesn't answer your question, but it might gives some intuition as to why this is true. Given the fact that there exists a solution to the equation $x^2-Py^2=-1$ when $P\equiv 1(\mod 4)$, one sees that the matrix $$ \begin{pmatrix}x & Py \\\ y & x\end{pmatrix} $$ fixes $\pm\sqrt{P}$ (under the action of $PGL_2(\mathbb{Z})$ on $\mathbb{RP}^1=\partial_{\infty} \mathbb{H}^2$). The conjugacy class of a primitive matrix in $GL_2(\mathbb{Z})$ (which is not reducible or finite order) is determined by the closed geodesic on the modular orbifold that it represents. This in turn is determined by a sequence of triangles which the geodesic crosses in the Farey graph: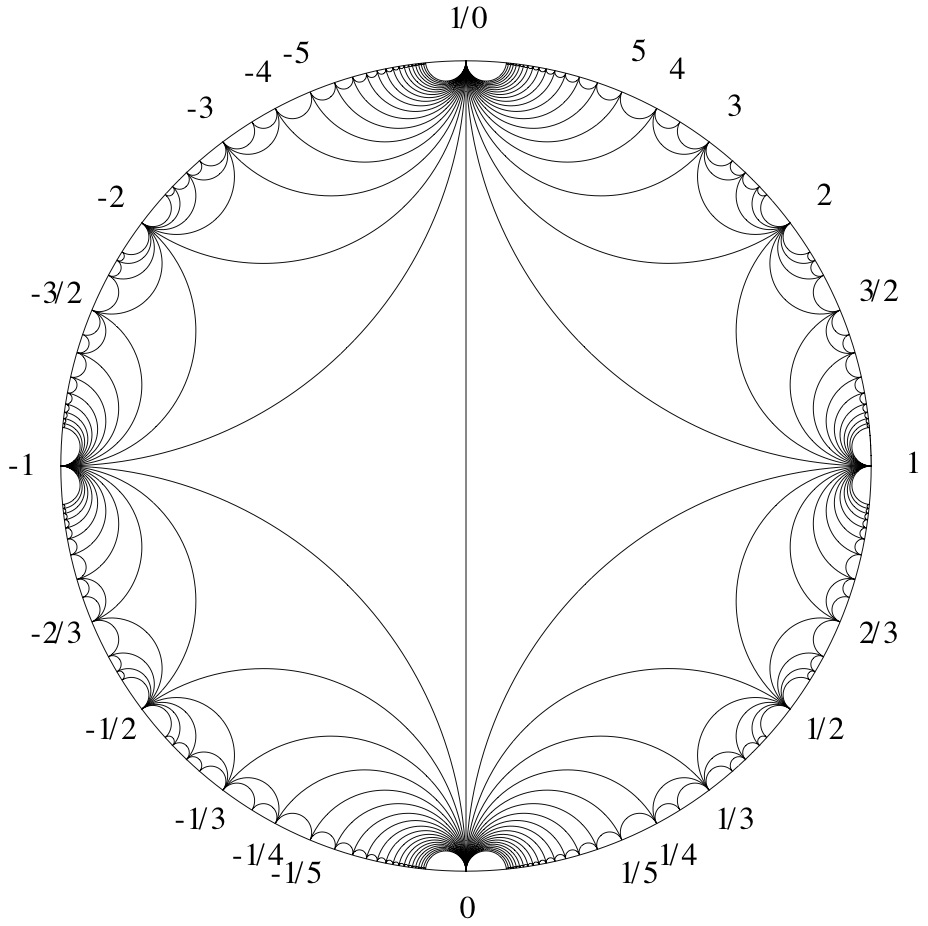
These triangles come in bunches sharing a common vertex, where the number in each bunch corresponds to coefficients of the continued fraction expansion.
The matrix is conjugate to $$\pm \left[\begin{array}{cc}1 & a_1 \\\ 0 & 1\end{array}\right] \left[\begin{array}{cc}1 & 0 \\\ a_2 & 1\end{array}\right] \cdots \left[\begin{array}{cc}1 & a_{2n} \\\ 0 & 1\end{array}\right]$$ if the determinant is 1, and to
$$\pm \left[\begin{array}{cc}1 & a_1 \\\ 0 & 1\end{array}\right] \left[\begin{array}{cc}1 & 0 \\\ a_2 & 1\end{array}\right] \cdots \left[\begin{array}{cc}1 & 0 \\\ a_{2n-1} & 1\end{array}\right] \left[\begin{array}{cc}0 & 1 \\\ 1 & 0\end{array}\right] $$ if the determinant is $-1$.
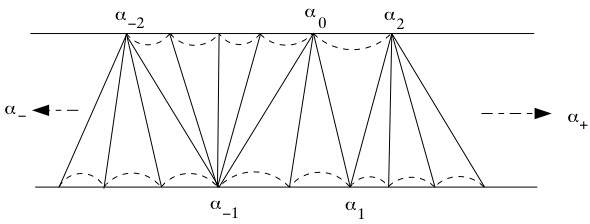
[Remark: the labels in this figure don't quite correspond to the matrices - it should be $a_i$'s instead of $\alpha_i$'s, and $\alpha_{\pm}$ should be $\pm\sqrt{P}$]
The number of such factors corresponds precisely to the period of the continued fraction expansion of fixed points of the matrix, since the closed geodesic is asymptotic in $\mathbb{H}^2$ to the geodesic connecting $\infty$ to $\sqrt{P}$, whose Farey sequence gives rise to the continued fraction expansion of $\sqrt{P}$. This number is even if and only if the matrix is orientation preserving, which is if and only if the determinant is 1. So the determinant is $1$ if and only if the continued fraction has even period, and the determinant is $-1$ if and only if the continued fraction has odd period, corresponding to $P\equiv 1(\mod 4)$.