It is known that the minimum solution of Pell's equation $x^2-dy^2=\pm1$ can be found from the continued fraction expansion of $\sqrt d$. Are there other methods for finding the minimum (or any other) solutions?
[Math] Methods for solving Pell’s equation
diophantine equationsnt.number-theory
Related Solutions
This doesn't answer your question, but it might gives some intuition as to why this is true. Given the fact that there exists a solution to the equation $x^2-Py^2=-1$ when $P\equiv 1(\mod 4)$, one sees that the matrix
$$
\begin{pmatrix}x & Py \\\ y & x\end{pmatrix}
$$
fixes $\pm\sqrt{P}$ (under the action of $PGL_2(\mathbb{Z})$ on $\mathbb{RP}^1=\partial_{\infty} \mathbb{H}^2$). The conjugacy class of a primitive matrix in $GL_2(\mathbb{Z})$ (which is not reducible or finite order) is determined by the closed geodesic on the modular orbifold that it represents. This in turn is determined by a sequence of triangles which the geodesic crosses in the Farey graph:
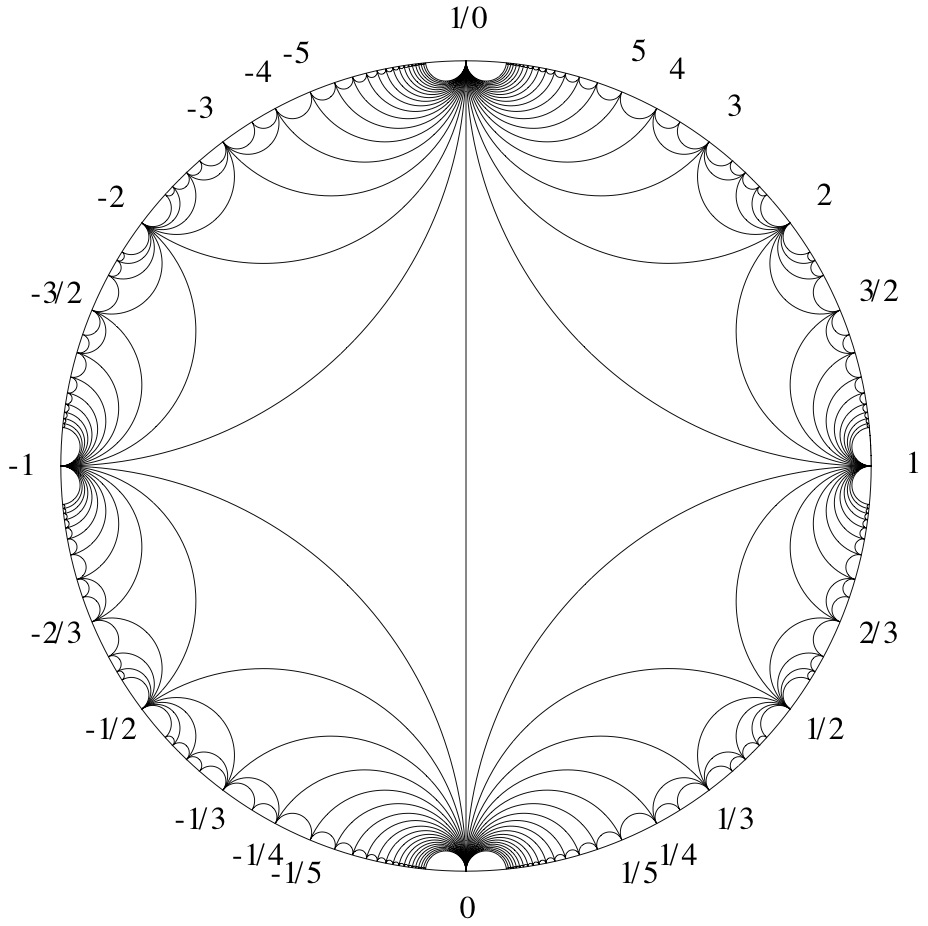These triangles come in bunches sharing a common vertex, where the number in each bunch corresponds to coefficients of the continued fraction expansion.
The matrix is conjugate to $$\pm \left[\begin{array}{cc}1 & a_1 \\\ 0 & 1\end{array}\right] \left[\begin{array}{cc}1 & 0 \\\ a_2 & 1\end{array}\right] \cdots \left[\begin{array}{cc}1 & a_{2n} \\\ 0 & 1\end{array}\right]$$ if the determinant is 1, and to
$$\pm \left[\begin{array}{cc}1 & a_1 \\\ 0 & 1\end{array}\right] \left[\begin{array}{cc}1 & 0 \\\ a_2 & 1\end{array}\right] \cdots \left[\begin{array}{cc}1 & 0 \\\ a_{2n-1} & 1\end{array}\right] \left[\begin{array}{cc}0 & 1 \\\ 1 & 0\end{array}\right] $$ if the determinant is $-1$.
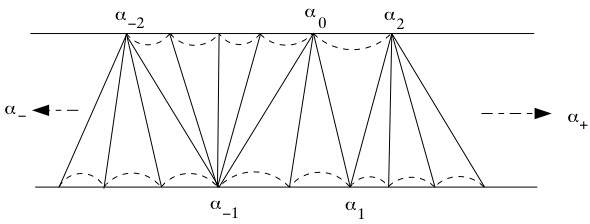
[Remark: the labels in this figure don't quite correspond to the matrices - it should be $a_i$'s instead of $\alpha_i$'s, and $\alpha_{\pm}$ should be $\pm\sqrt{P}$]
The number of such factors corresponds precisely to the period of the continued fraction expansion of fixed points of the matrix, since the closed geodesic is asymptotic in $\mathbb{H}^2$ to the geodesic connecting $\infty$ to $\sqrt{P}$, whose Farey sequence gives rise to the continued fraction expansion of $\sqrt{P}$. This number is even if and only if the matrix is orientation preserving, which is if and only if the determinant is 1. So the determinant is $1$ if and only if the continued fraction has even period, and the determinant is $-1$ if and only if the continued fraction has odd period, corresponding to $P\equiv 1(\mod 4)$.
If you had a fast method for solving Pell equations $x^2 - dy^2 =1$, you can factor numbers $N$ quickly: all you have to do is compute gcd$(x-1,d)$ for $d = N, 2N, 3N, \ldots$ until you find a factor; if the factor is not prime, repeat the procedure.
Schoof showed that you don't have to know the actual solution of the Pell equation, but that the size of the regulator is sufficient. His method uses Shanks' idea of infrastructure (see e.g. Jacobson and Williams, Solving the Pell Equation). By computing an ambiguous ideal (if the norm of the fundamental unit is positive) he can then factor $d = N$; if the ambiguous ideal is trivial, do the same for $d = 3N$ etc.
Of course you cannot expect to factor Fermat numbers by simply writing down a solution of the corresponding Pell equation. In the early days of factoring in the 1970s, Brillhart and Morrison suggested using small multiples of $N$ if the period of the continued fraction of $\sqrt{N}$ is too small - this hasn't changed.
Best Answer
The basic and classical methods, apart from brute force, are
continued fraction expansions (regular, nearest integer, etc.) or, equivalently, some form of reduction theory for indefinite binary quadratic forms;
computing many elements of small norm in a quadratic number field, which often is a lot more effective; the technique used here is also used for factoring integers.
For a detailed algorithmic description see Jacobson & Williams (Solving the Pell Equation) or Buchmann & Vollmer (Binary Quadratic Forms).
In addition, you can compute a power of the fundamental unit from the class number formulas, which essentially consists in taking norms of suitable cyclotomic units. Kronecker has shown how to solve the Pell equation using elliptic and modular functions, and Girstmair (Kronecker's solution of the Pell equation on a computer {Kroneckers Lösung der Pellschen Gleichung auf dem Computer], Math. Semesterber. 53, 45-64 (2006)) has shown that it can be made to work in practice.
You can also imitate the theory of descent on elliptic curves; I have sketched connections with classical tricks in some preprints on higher descent on Pell conics.