I'm trying to work out a proof for the following proposition:
Let $A \in \mathbb{R}^{n,n}$ a real, symmetric matrix with eigenvalues $\lambda_1 \ge \lambda_2 \ge \cdots \ge \lambda_n$, then
$$\max \lbrace {\rm tr} ( V^t A V ) \mid V \in \mathbb{R}^{n,k}, \, V^t V={\rm Id}_k \rbrace = \sum\limits_{i=1}^k \lambda_k $$
I've already found a proof myself which I've posted at the end of this question. However, I feel I've still missed a very important point: This theorem should be a direct consequence of the min/max– or Courant-Fischer-characterization of eigenvalues (https://en.wikipedia.org/wiki/Min-max_theorem). Although, after realizing that $\text{tr}(V^TAV) = \sum_{i=1}^k <Av_i,v_i>$, this approach looks very promising, I was not able to continue the proof.
For $k=1$ the statement is directly proven by Courant-Fischer. For other values of $k$ inductive reasing comes to mind. However, it is not clear to me, why this 'greedy approach' (maximize $k-1$ summands first and then choose the $k$-th accordingly) reaches the true maximum and how the minimum of the Courant-Fischer characterization isn't an issue.
I'd be very thankful for hints and solutions!
different proof without min/max-theorem:
Choose an orthonormal basis consisting of eigenvectors, writeall $v_i$'s in this representation and calculate
$\text{tr}(V^TAV) = \sum_{i=1}^n \lambda_i (\sum_{j=1}^k \alpha_{i,j}^2) = \sum_{i=1}^n h_i \lambda_i$
with $h_i := \sum_{j=1}^k \alpha_{i,j}^2$. Since $V^TV=\text{Id}_k$ we have $0 \le h_i \le 1$ and $\sum_{i=1}^n=k$. This shows that the maximum is attained for $h_1 = … = h_k =1$ and $h_{k+1} = … = h_n = 0$, which proofs the claim.

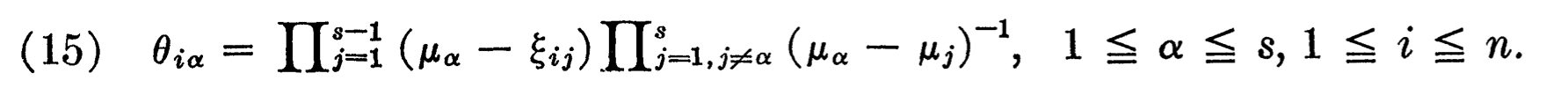
Best Answer
As you pointed out we have $$tr(V^T A V) = \sum_{i=1}^k \langle A v_i, v_i \rangle$$
Our restraints are $\langle v_i, v_i \rangle = 1$ and $\langle v_i, v_j \rangle = 0$.
Now suppose we took a greedy approach, and tried to maximize $\langle A v_1, v_1 \rangle$ first, and then maximimize $\langle A v_2, v_2 \rangle$ subject to the constraint that $\langle v_1, v_2 \rangle = 0$ and so on. Then by min-max C-F, we would have $\langle A v_1, v_1\rangle = \lambda_1$, and $\langle A v_i, v_i \rangle \geq \lambda_i$ for each $i$. Hence this approach would yield the fact that $\max tr(V^T A V) \geq \sum_1^k \lambda_i$.
This reduces the problem to showing that $tr(V^T A V) \leq \sum_1^k \lambda_i$ for all choices of $v_i$. This is equivalent to the fact that the diagonal entries of $A$ are majorized by the eigenvalues of $A$, a statement proved in https://en.wikipedia.org/wiki/Schur%E2%80%93Horn_theorem.
I am not aware of a version of the second fact that relies on C-F, although it might exist.