Several ancient arguments suggest a curved Earth, such as
the observation that ships disappear mast-last over the
horizon, and
Eratosthenes'
surprisingly accurate calculation of the size of the
Earth
by measuring a difference in shadow length between
Alexandria and Syene. These observations, however, suggest
merely a curved Earth rather than a spherical one.
Another ancient argument specifically suggesting a
spherical Earth is the fact that the shadow of the Earth on
the moon during a Lunar eclipse is circular.
My question is: is it true that the sphere is
the only surface all of whose projections are disks?
It surely seems to be true. The corresponding fact,
however, is not true in two dimensions. The Reuleaux
triangle
pictured below is a figure of constant
width,
meaning that every projection of it in the plane is a line
segment of the same length.
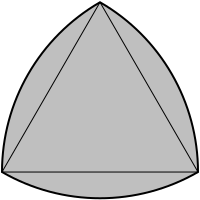
There are also surfaces of constant
width
in higher dimensions, meaning that any two parallel
bounding set of hyperplanes (touching the boundary) have
constant separation. But all of the non-spherical examples
of such surfaces I have seen have obviously non-circular
projections.
It also seems clear that finitely many circular projections
is insufficient, since intersecting finitely many cylinders
would produce a surface having corners and containing some
straight line segments.
The fact that you can spin such a surface with all circular
projections inside any bounding cylinder is suggestive, but it
is also true that you can spin the Reuleaux triangle
inside a square,
even though it isn't circular.
Further questions would include:
- To what extent are other surfaces determined by their
projections? That is, which other shapes can we recognize
by the set of their shadows? - In particular, can we recognize the cube and other regular solids by their shadows?
- Which sets of shadows are realizable as projections of a
surface? Is there some way to characterize these sets?
Clearly they must be continuously deformable to one
another and obey several other obvious conditions.
We had a great time discussing the question after our logic
seminar here in New York this week, when our speaker
Maryanthe Malliaris asked
the spherical Earth question.
December 20, 2010: In light (or dark, as it were) of the lunar eclipse tonight, I am bumping this question, with the remark also that despite the truly outstanding answers we have received, several of the further questions stated above are not fully answered.

Best Answer
The answer to the title question is yes (well, I assume that by a "surface" you mean something reasonable, like a boundary of a convex set).
Let $AB$ be the longest segment with endpoints on the surface. We may assume that its length equals 2 and its midpoint is the origin. Consider projections to the planes that contain $AB$. Since projections do not increase distances, $AB$ is a diameter of each projection. Hence all projections to this family of planes are unit discs centered at the origin. The intersection of the corresponding cylinders is the unit ball, hence the result.
Added. In general, we cannot determine a convex body from the set of shadows (if we don't know the correspondence between shadows and directions of projections).
Take a unit ball and cut off three identical tiny caps whose centers form a regular triangle on the sphere and are not on one great circle. Looking at shadows, you cannot tell whether all three or only two caps are removed, because each projection shows you no more than two of them.
The same construction works for polyhedra if you start with an icosahedron rather than a ball.