Edit: Here is what I think is a counter-example.
Let $\phi$ be the indication function of the even natural numbers, let $\mathcal U$ be an ultrafilter supported on the even naturals, and let $\mathcal V$ be an ultrafilter defined on the even negative integers. Define $\mu\in M(\mathbb Z)$ by
$$\int f(x) \ d\mu(x) = \lim_{x\in\mathcal V} f(x).$$
Then $\mu\in I_\phi$ (as, in fact, $\int \phi(x+y) \ d\mu(y)=0$ for all $x$). If $\nu\in I_\phi$ then $\nu$ must assign the same measure to $2\mathbb N$ and $2\mathbb N+1$, say $\alpha\leq 1/2$. You also need to argue that $\nu$ must assign zero measure to any finite set (else it won't be $\phi$-invariant). So for any $y\in\mathbb Z$,
$$\int \phi(x+y) \ d\nu(x) = \nu(2\mathbb N-y) = \begin{cases}
\nu(2\mathbb N) &: y\in 2\mathbb Z, \\ \nu(2\mathbb N+1) &: y\in 2\mathbb Z+1, \end{cases}
= \alpha.$$
Thus
$$\int \int \phi(x+y) \ d\nu(x) \ d\mu(y) = \int \alpha \ d\mu(y) = \alpha,$$
as $\mu$ is a probability measure. By contrast, let $\nu$ be defined by
$$\int f(x) \ d\nu(x) = \lim_{y\in\mathcal U} f(y).$$
Then
$$\int \phi(x+y) \ d\nu(x) = \begin{cases} 1 &: y\in 2\mathbb Z, \\
0 &: y \in 2\mathbb Z+1, \end{cases}$$
and so
$$\int \int \phi(x+y) \ d\nu(x) \ d\mu(y) = \int \chi_{2\mathbb Z}(y) \ d\mu(y)
= 1.$$
So $F$ is not maximised on $I_\phi$.
In fact, by replacing $2\mathbb N$ by $k\mathbb N$, I think you get that $F$ has norm one, but $F(\nu)\leq 1/k$ for any $\nu\in I_\phi$.
But somehow, to my mind, what's wrong is that the $\mu\in I_\phi$ you choose is very poor. So here's a revised conjecture:
Let $\mu\in I_\phi$ maximise the integral $\int \phi(x) \ d\mu(x)$. Then $F$ attains its maximum on $I_\phi$.
Old post: (Explains my thinking).
I think of these questions using the Arens products, from abstract Banach algebra theory. So I work over the complex numbers; but this is not a problem.
Consider $A=\ell^1(\mathbb Z)$ with the convolution product, so $A$ is commutative. Then $A^*=\ell^\infty(\mathbb Z) = C(\beta\mathbb Z)$ is an $A$-module: $(a\cdot f)(b) = f(ba)$ for $a,b\in A,f\in A^*$. Then $A^{**}=M(\beta\mathbb Z)$ the space of finite Borel measures on the Stone-Cech compactification $\beta\mathbb Z$. Your space $M(\mathbb Z)$ is just the positive measures $\mu\in A^{**}$ with $\mu(1)=1$.
We try to extend the product of $A$ to $A^{**}$. Firstly we define a bilinear map $A^{**}\times A^*\rightarrow A^*$ by
$$(\mu\cdot f)(a) = \mu(a\cdot f) \qquad (\mu\in A^{**}, f\in A^*, a\in A).$$
But then we have two choices for the product on $A^{**}$:
$$(\mu \Box \lambda)(f) = \mu(\lambda\cdot f), \quad
(\mu\diamond\lambda)(f) = \lambda(\mu\cdot f)
\qquad (\mu,\lambda\in A^{**}, f\in A^*).$$
A little thought shows that $\mu\diamond\lambda = \lambda\Box\mu$.
So if $\phi\in A^*$ if positive then $\mu\in I_\phi$ if and only if $\mu\cdot\phi
= \mu(\phi) 1$. This follows, as writing $\delta_x\in A=\ell^1(\mathbb Z)$ for the point mass at $x\in\mathbb Z$, we have
$$(\phi\cdot\delta_x)(\delta_y) = \phi(\delta_{x+y}) \implies
(\mu\cdot\phi)(\delta_x) = \mu(\phi\cdot\delta_x)
= \int \phi(x+y) \ d\mu(y).$$
So the condition that $\mu\in I_\phi$ becomes that $(\mu\cdot\phi)(\delta_x)$ is constant in $x$, which is seen to be equivalent to $\mu\cdot\phi = \mu(\phi) 1$.
Similarly, your map $F$ is just $F(\nu) = (\mu\Box\nu)(\phi)$.
As you allude to, it's known that $\lambda\Box\mu \not= \mu\Box\lambda$ for arbitrary $\lambda,\mu$. However, we say that $f\in A^*$ is "weakly almost periodic" (WAP) if $(\lambda\Box\mu)(f) = (\mu\Box\lambda)(f)$ for all $\mu,\lambda\in A^{**}$. So if $\phi$ is WAP and $\mu\in I_\phi$ then for any $\nu\in M(\mathbb Z)$,
$$F(\nu) = (\mu\Box\nu)(\phi) = (\nu\Box\mu)(\phi) = \nu(\mu\cdot\phi)
= \nu(1) \mu(\phi) = \mu(\phi),$$
as $\nu$ is a probability measure. So actually $F$ is constant on $M(\mathbb Z)$ and so certainly attains its maximum at a point of $I_\phi$.
So, to be interesting, we need to ask the question for $\phi$ which are not WAP. An alternative characterisation of $\phi$ being in WAP is that the set of translates of $\phi$ in $\ell^\infty(\mathbb Z)$ forms a relatively weakly compact set. A nice characterisation of Grothendieck shows that this is equivalent to
$$\lim_n \lim_m \phi(x_n+y_m) = \lim_m \lim_n \phi(x_n+y_m)$$
whenever all the limits exist, for sequences $(x_n),(y_m)$ in $\mathbb Z$. If $\phi$ is the indicator function of $\mathbb N$, then it's not in WAP.
We may as well assume that $\|\phi\|_\infty=1$.
Another "easy" case is when we can find $\nu\in I_\phi$ with $\nu(\phi)=1$. Then $F(\nu) = \mu(\nu\cdot\phi) = \mu(1) \nu(\phi) = 1$; while for any $\lambda\in M(\mathbb Z)$, clearly $|F(\lambda)| = |\mu(\lambda\cdot\phi)| \leq 1$ as $\mu$ is a probability measure, and $\lambda\cdot\phi$ is bounded by $1$ (again, as $\lambda$ is a probability measure and $\phi$ is bounded by $1$). Notice that this case covers your example of when $\phi$ is the indicator function of $\mathbb N$.
So a test case is to find $\phi$ not in WAP and with $\nu(\phi)<\|\phi\|_\infty$ for all $\nu\in I_\phi$ (notice that $I_\phi$ is always non-empty, as $\mathbb Z$ is amenable). Do you have an example of such a $\phi$?
Actually, if $\phi$ is the indicator function of the even natural numbers, then that's an example. And that leads to my (hopeful) counter-example.
With apologies for promoting my own work, there's a whole book on the
mathematics of the exponentials of various entropies:
Tom Leinster, Entropy and Diversity: The Axiomatic
Approach. Cambridge University Press, 2021.
You can download a free copy by clicking, although persons of taste will
naturally want to grace their bookshelves with the bound work.
The direct answer to your literal question is that I don't know of a
compelling geometric interpretation of the exponential of entropy. But the
spirit of your question is more open, so I'll explain (1) a non-geometric
interpretation of the exponential of entropy, and (2) a geometric
interpretation of the exponential of maximum entropy.
Diversity as the exponential of entropy
As Carlo Beenakker says, the exponential of entropy (Shannon or more
generally Rényi) has long been used by ecologists to quantify biological
diversity. One takes a community with $n$ species and writes $\mathbf{p} =
(p_1, \ldots, p_n)$ for their relative abundances, so that $\sum p_i =
1$. Then $D_q(\mathbf{p})$, the exponential of the Rényi entropy of
$\mathbf{p}$ of order $q \in [0, \infty]$, is a measure of the
diversity of the community, or "effective number of species" in the
community.
Ecologists call $D_q$ the Hill number of order $q$, after
the ecologist Mark Hill, who introduced them in 1973 (acknowledging the
prior work of Rényi). There is a precise mathematical sense in which the
Hill numbers are the only well-behaved measures of diversity, at least if one
is modelling an ecological community in this crude way. That's Theorem
7.4.3 of my book. I won't talk about that here.
Explicitly, for $q \in [0, \infty]$
$$
D_q(\mathbf{p}) = \biggl( \sum_{i:\,p_i \neq 0} p_i^q \biggr)^{1/(1 - q)}
$$
($q \neq 1, \infty$). The two exceptional cases are defined by taking limits
in $q$, which gives
$$
D_1(\mathbf{p}) = \prod_{i:\, p_i \neq 0} p_i^{-p_i}
$$
(the exponential of Shannon entropy) and
$$
D_\infty(\mathbf{p}) = 1/\max_{i:\, p_i \neq 0} p_i.
$$
Rather than picking one $q$ to work with, it's best to consider all of
them. So, given an ecological community and its abundance distribution
$\mathbf{p}$, we graph $D_q(\mathbf{p})$ against $q$. This is called the
diversity profile of the community, and is quite informative. As Carlo
says, different values of the parameter $q$ tell you different things about
the community. Specifically, low values of $q$ pay close attention to
rare species, and high values of $q$ ignore them.
For example, here's the diversity profile for the global community of great
apes:
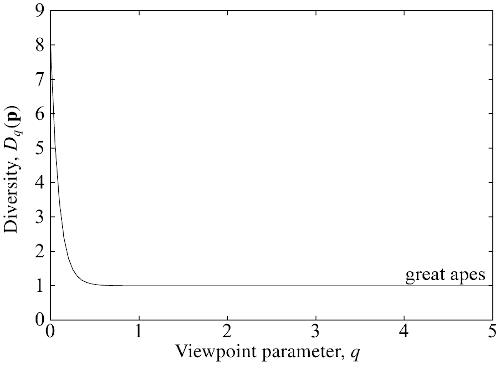
(from Figure 4.3 of my book). What does it tell us? At least two things:
The value at $q = 0$ is $8$, because there are $8$ species of great ape
present on Earth. $D_0$ measures only presence or absence, so that a
nearly extinct species contributes as much as a common one.
The graph drops very quickly to $1$ — or rather, imperceptibly more
than $1$. This is because 99.9% of ape individuals are of a single
species (humans, of course: we "outcompeted" the rest, to put it diplomatically). It's only the very
smallest values of $q$ that are affected by extremely rare
species. Non-small $q$s barely notice such rare species, so from their
point of view, there is essentially only $1$ species. That's why
$D_q(\mathbf{p}) \approx 1$ for most $q$.
Maximum diversity as a geometric invariant
A major drawback of the Hill numbers is that they pay no attention to how
similar or dissimilar the species may be. "Diversity" should depend on the
degree of variation between the species, not just their
abundances. Christina Cobbold and I found a natural generalization of the Hill
numbers that factors this in — similarity-sensitive diversity
measures.
I won't give the definition (see that last link or Chapter 6 of the book),
but mathematically, this is basically a definition of the entropy or
diversity of a probability distribution on a metric space. (As before,
entropy is the log of diversity.) When all the distances are $\infty$, it
reduces to the Rényi entropies/Hill numbers.
And there's some serious geometric content here.
Let's think about
maximum diversity. Given a list of species of known similarities to one
another — or mathematically, given a metric
space — one can ask what the maximum possible value of the diversity
is, maximizing over all possible species distributions $\mathbf{p}$. In other words,
what's the value of
$$
\sup_{\mathbf{p}} D_q(\mathbf{p}),
$$
where $D_q$ now denotes the similarity-sensitive (or metric-sensitive)
diversity? Diversity is not usually maximized by the uniform distribution
(e.g. see Example 6.3.1 in the book), so the question is not trivial.
In principle, the answer depends on $q$. But magically, it doesn't! Mark
Meckes and I proved this. So
$$
D_{\text{max}}(X) := \sup_{\mathbf{p}} D_q(\mathbf{p})
$$
is a well-defined real invariant of finite metric spaces $X$, independent
of the choice of $q \in [0, \infty]$.
All this can be extended to compact metric spaces, as Emily Roff and I
showed. So every compact metric space
has a maximum diversity, which is a nonnegative real number.
What on earth is this invariant? There's a lot we don't yet know, but we do
know that maximum diversity is closely related to some classical geometric
invariants.
For instance, when $X \subseteq \mathbb{R}^n$ is compact,
$$
\text{Vol}(X)
=
n! \omega_n
\lim_{t \to \infty}
\frac{D_{\text{max}}(tX)}{t^n},
$$
where $\omega_n$ is the volume of the unit $n$-ball and $tX$ is $X$ scaled
by a factor of $t$. This is Proposition 9.7 of my paper with
Roff and follows from work of Juan
Antonio Barceló and Tony Carbery. In short: maximum diversity determines
volume.
Another example: Mark Meckes showed that the Minkowski dimension of a
compact space $X \subseteq \mathbb{R}^n$ is given by
$$
\dim_{\text{Mink}}(X)
=
\lim_{t \to \infty}
\frac{D_{\text{max}}(tX)}{\log t}
$$
(Theorem 7.1 here). So, maximum diversity
determines Minkowski dimension too.
There's much more to say about the geometric aspects of maximum
diversity. Maximum diversity is closely related to another recent invariant of
metric spaces, magnitude. Mark
and I wrote a survey paper on the more
geometric and analytic aspects of magnitude, and you can find more on all
this in Chapter 6 of my book.
Postscript
Although diversity is closely related to entropy, the diversity viewpoint really opens up new mathematical questions that you don't see from a purely information-theoretic standpoint. The mathematics of diversity is a rich, fertile and underexplored area, waiting for mathematicians to come along and explore it.

Best Answer
I don't know if someone has already defined such entropy and I am not an expert on these things, but (depending what is wanted) I would start with something like $$E(\mu)=\sup\left\{-\sum_{i=1}^n\mu(A_i)\log(\mu(A_i)) : \mathbb{N} = \bigcup_{i=1}^n A_i, A_i \text{ pairwise disjoint}\right\}.$$
Some properties this entropy would have are
A related definition for arbitrary measure spaces $(X,m)$ is the relative Shannon entropy (a.k.a. the Kullback–Leibler divergence) $$E(\mu) = \int_X \frac{d\mu}{dm} \log\left(\frac{d\mu}{dm}\right)dm,$$ where $\frac{d\mu}{dm}$ is the Radon-Nikodym derivative of $\mu$ w.r.t. $m$. One could fix a finitely additive measure $m$ and try to work with that.