In his Huygens and Barrow, Newton and Hooke, Arnold mentions a notorious teaser that, in his opinion, "modern" mathematicians are not capable of solving quickly. Then, he adds that the exception that proved the rule in this case of his was the German mathematician Gerd Faltings.
My question is whether any of you knows the complete story behind those lines in Arnold's book. I mean, did Arnold pose the problem somewhere (maybe Квант?) and Faltings was the only one that submitted a solution after Arnold's own heart? Is the previous conjecture totally unrelated to the actual development of things?
I thank you in advance for your insightful replies.
P.S. It seems that this teaser of Arnold eventually became a cult thingy in certain branches of the Russian mathematical community. Below you can find a photograph taken by a fellow of mine of one of the walls of IUM's cafeteria (where IUM stands for Independent University of Moscow). As the Hindu mathematician Bhāskara would say (or so the legend has it): BEHOLD!
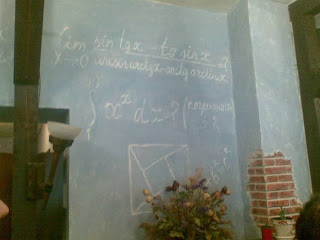
Best Answer
Here is a problem which I heard Arnold give in an ODE lecture when I was an undergrad. Arnold indeed talked about Barrow, Newton and Hooke that day, and about how modern mathematicians can not calculate quickly but for Barrow this would be a one-minute exercise. He then dared anybody in the audience to do it in 10 minutes and offered immediate monetary reward, which was not collected. I admit that it took me more than 10 minutes to do this by computing Taylor series.
This is consistent with what Angelo is describing. But for all I know, this could have been a lucky guess on Faltings' part, even though he is well known to be very quick and razor sharp.
The problem was to find the limit
$$ \lim_{x\to 0} \frac { \sin(\tan x) - \tan(\sin x) } { \arcsin(\arctan x) - \arctan(\arcsin x) } $$
The answer is the same for $$ \lim_{x\to 0} \frac { f(x) - g(x) } { g^{-1}(x) - f^{-1}(x) } $$ for any two analytic around 0 functions $f,g$ with $f(0)=g(0)=0$ and $f'(0)=g'(0)=1$, which you can easily prove by looking at the power expansions of $f$ and $f^{-1}$ or, in the case of Barrow, by looking at the graph.
End of Apr 8 2010 edit
Beg of Apr 9 2012 edit
Here is a computation for the inverse functions. Suppose $$ f(x) = x + a_2 x^2 + a_3 x^3 + \dots \quad \text{and} \quad f^{-1}(x) = x + A_2 x^2 + A_3 x^3 + \dots $$
Computing recursively, one sees that for $n\ge2$ one has $$ A_n = -a_n + P_n(a_2, \dotsc, a_{n-1} ) $$ for some universal polynomial $P_n$.
Now, let $$ g(x) = x + b_2 x^2 + b_3 x^3 + \dots \quad \text{and} \quad g^{-1}(x) = x + B_2 x^2 + B_3 x^3 + \dots $$
and suppose that $b_i=a_i$ for $i\le n-1$ but $b_n\ne a_n$. Then by induction one has $B_i=A_i$ for $i\le n-1$, $A_n=-a_n+ P_n(a_2,\dotsc,a_{n-1})$ and $B_n=-b_n+ P_n(a_2,\dotsc,a_{n-1})$.
Thus, the power expansion for $f(x)-g(x)$ starts with $(a_n-b_n)x^n$, and the power expansion for $g^{-1}(x)-f^{-1}(x)$ starts with $(B_n-A_n)x^n = (a_n-b_n)x^n$. So the limit is 1.