On the Wolfram page about the Euler-Mascheroni Constant $\gamma $, the following amazing limit is given without proof (referring to "personal communication"):
$$\lim_{z\to\infty}\left[\zeta(\zeta(z))-2^z+\Bigl(\frac43\Bigr)^z\right]=\gamma -1$$
I have checked to thousands of decimals that likewise $$\lim_{z\to\infty}\left[\zeta\Bigl(\frac1{\zeta(z)}\Bigr)+2^z-\Bigl(\frac43\Bigr)^z\right]=\gamma $$ and started wondering what happens if we combine both, e.g. by fixing a weight $0\leqslant\lambda\leqslant1$ and looking at the behaviour of $$ f_\lambda(z):=\zeta \Bigl(\lambda{\zeta(z)+\frac{1-\lambda}{\zeta(z)}}\Bigr) $$ for again growing $z$ on the real axis. So the argument in the big parenthesis still tends to $1$, such that the pole at $\zeta(1)$ is approached in different ways depending on $\lambda$. And something cute happens: Numerically it looks like $$\boxed{\color{blue}{ \lim_{z\to\infty}\left[f_{\lambda}(z)- \frac1{2\lambda-1}\left(2^z- \Bigl(\frac43\Bigr)^z\right) \right]=\gamma -\frac{\lambda}{(2\lambda-1)^2}}}$$ for $\lambda\ne\frac12$ (even outside the interval $[0,1]$), while, completely off, $$ f_{1/2}(z)\sim 2\cdot4^z-4\cdot\Bigl(\frac83\Bigr)^z -2\cdot 2^z -\text {(5 other exp terms)}-4+\gamma. $$
I am wondering if such a formula has appeared before and how to prove it!
Best Answer
The paper entitled Euler constant as a renormalized value of Riemann zeta function at its pole by Andrei Vieru contains a derivation of the first formula in the OP (Benoȋt Cloitre's formula), and a method to obtain variations thereof, such as

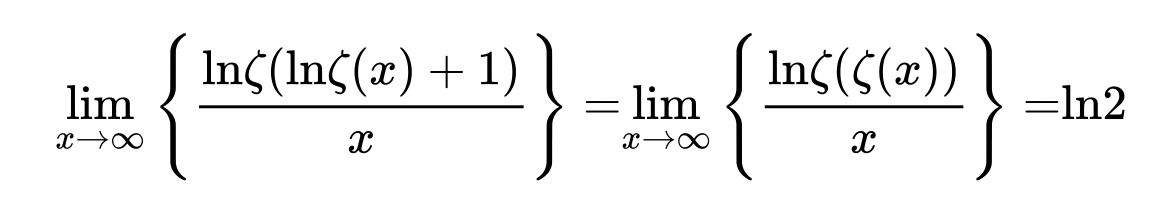
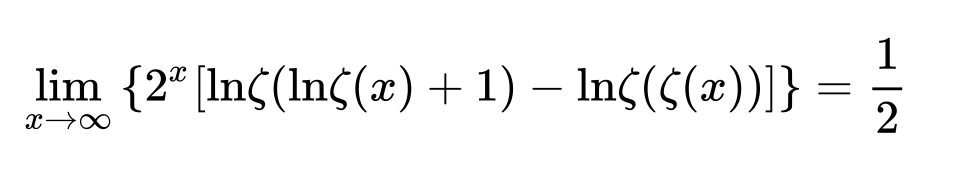
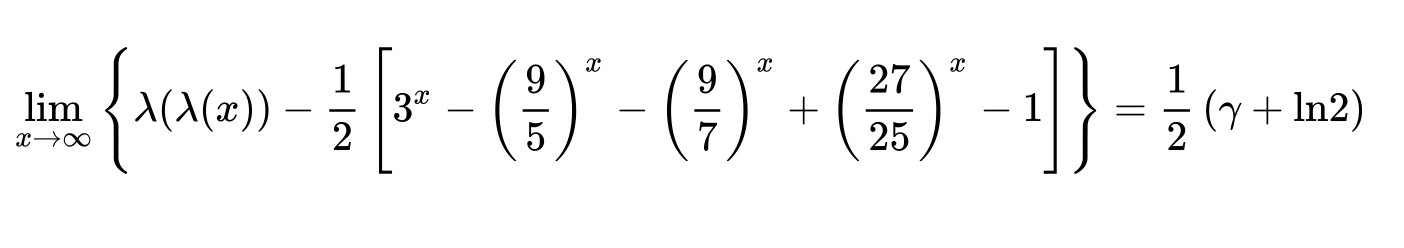
as well as similar iterates in terms of the Dirichlet function $\lambda(s)=\sum_{n=0}^\infty(2n+1)^{-s}$,