Why does least-squares need regularization

least squareslinear regressionoptimizationregularization

If I understand regularization correctly, it helps if a least-squares problem is not well-posed thus…

  1. the problem has no solution

  2. the problem has multiple solutions

  3. a small change in the input leads to a large change in the output

Let's say that for our regression problem $X\beta=y$ the matrix $X$ has full rank, isn't the least squares solution $\beta = (X^* X)^{-1} X^* y$ always defined and always unique? Is this not correct or does regularization help with the 3rd condition?

Best Answer

Usually regularization is applied to regression problems that $X$ is a fat matrix (opposing to tall matrix), $N\times p$ where $p>N$, i.e. you have more predictors than data points.

Then in that case the original Least square solution $(X^TX)^{-1}X^Ty$ doesn't make sense, since $X^TX$ is at most rank $p$ thus degenerate and non-invertible. In the original problem $X\beta = y$ there are more than 1 solution: moving in the null space of $X$ won't change the solution $\beta\in \beta_0+null(X)$.

Then introducing a regularization term e.g. in Ridge, makes the least square formula invertible and unique again $$ \hat\beta_{ridge} = (X^TX+\lambda I)^{-1}X^Ty $$

You can argue this brings stability to the solution since adding $\lambda$ reduce the condition number of $(X^TX+\lambda I)$ which makes the inversion more numerically stable.

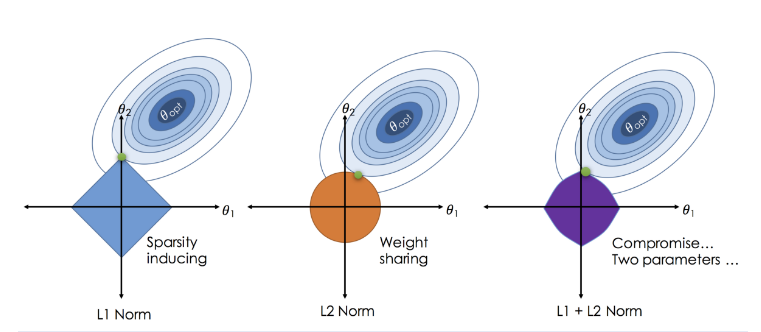
From a geometric viewpoint, we can also say the regularizations added an additional loss term to distinguish the solutions in the solution manifold ($\beta\in \beta_0+null(X)$), which makes the solution unique. (see this famous illustration of the loss landscape of regularized regression)

Related Question