So, as you can see in the photo above, I solved this equation and I got $2$ results as an answer. But my teacher stated that there actually are $3$ answers. The third one being $4\pi/3$. This occurs because, according to him: 
. When I use my calculator it only gave me back the number $2\pi/3$. With all of that being stated, how can it be that there are three different solutions for this equation if the highest exponent is $2$? I mean, isn't it that the highest exponent dictates the number of solutions that an equation has?.
P.S. In case that you are wondering, Solución means solution in Spanish.
Edit: en means in.
Best Answer
Your calculator only gives you $\frac{2\pi}{3}$ because they are certain domain restrictions that your calculator has to take into account when using the inverse trigonometric functions. Recall that a function can only have an inverse when it is one-to-one, so the only way to get an inverse for cosine is to restrict its domain. Since $\cos(0) = 1$ and $\cos(\pi) = -1$, if we restrict the domain of cosine to the interval $[0,\pi]$, then we have a one-to-one function, so it makes sense to talk about its inverse. Now, the domain of a function is the same as the range of its inverse, so the range of $\arccos(x)$ is $[0,\pi]$. This means that your calculator will only give you $\frac{2\pi}{3}$ and not $\frac{4\pi}{3}$, because $\frac{4\pi}{3}$ is not in the range of $\arccos(x)$.
Now recall the unit circle.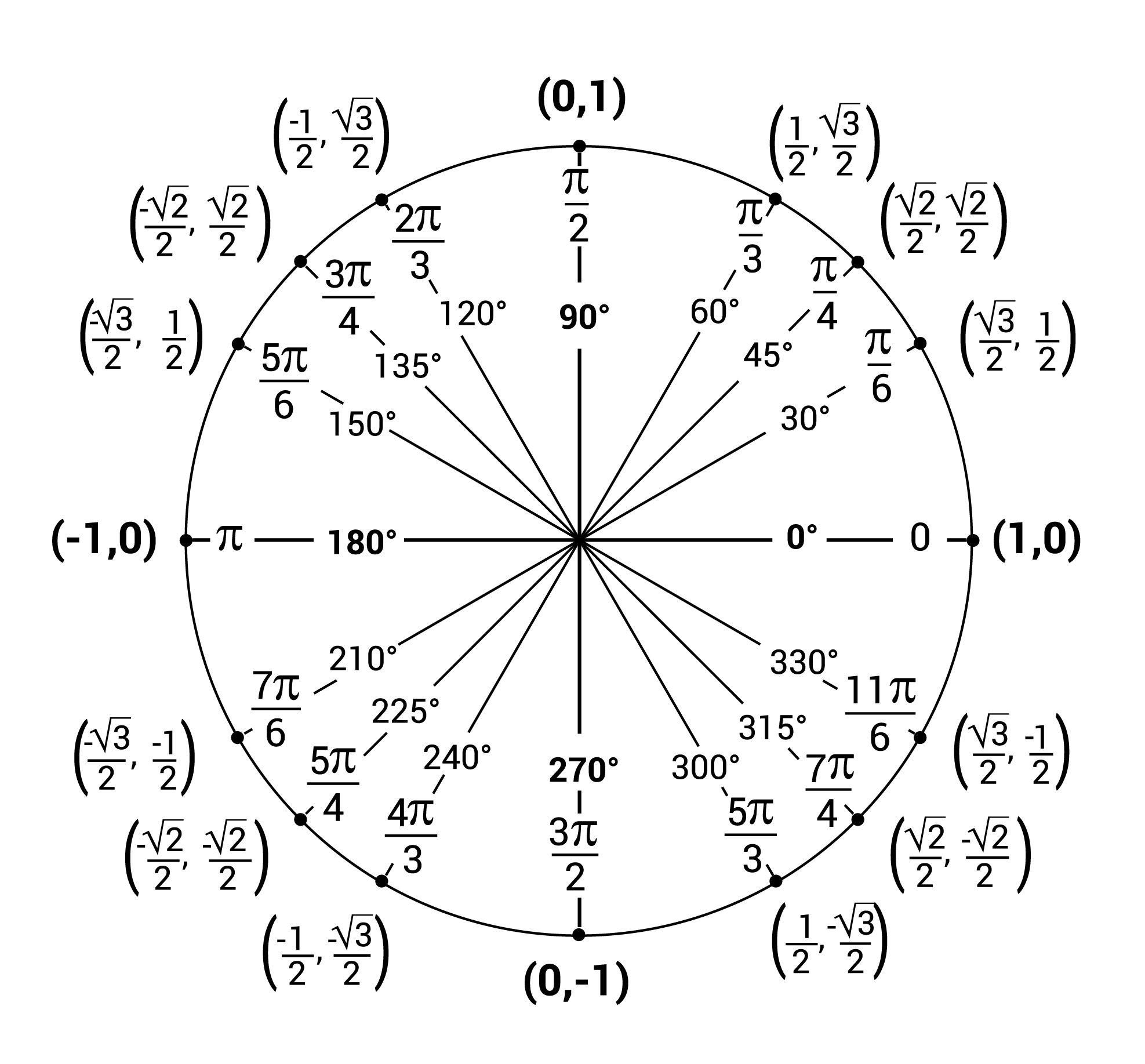
From this we can certainly see that $\cos\left(\frac{2\pi}{3}\right) = -\frac{1}{2}$, but we can also see that $\cos\left(\frac{4\pi}{3}\right) = -\frac{1}{2}$. In conclusion, be very familiar with the unit circle, it often comes in useful! Hope this helps!