Problem
Introduction
Question
The Mice Problem:
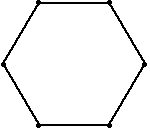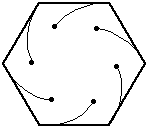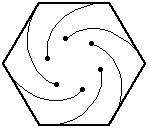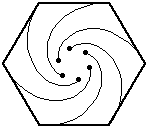
In the mice problem […] $n$ mice start at the corners of a regular $n$-gon of unit side length, each heading towards its closest neighboring mouse in a counterclockwise direction at constant speed. […] – Weisstein, Eric W. "Mice Problem." From MathWorld–A Wolfram Web Resource.
I would like to calculate the distance of the closest mice given a distance traveled $s$.
Background
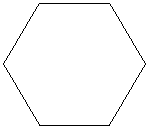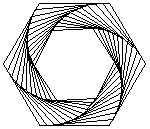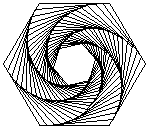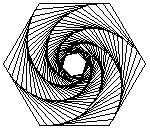
If you're wondering why I want to calculate this, I just read about the problem in Math World > History and Terminology Disciplinary Terminology Biological Terminology > Mise Problem. That's when I saw the animations of the mise and wanted to animate them too. The connection between this problem and the Whirl struck me, and that's when the question came up after the Whirl gave me a context.
With a few seconds of thinking I figured that position doesn't just depend on distance traveled, previous position and speed, so it should change to an ODE / PDE, which sounds like a fun project.
My Two Best Trys
Numerical Trys
A plot of the first $3$ steps ($\color{green}{\frac{1}{2}}$ distance and $\color{orange}{\frac{1}{4}}$ distance (for the first step)):
Are $\left( x_{1}, y_{1} \right)$ the coordinates of one mouse $a_{1}$ and $\left( x_{2}, y_{2} \right)$ those of the other, then $a_{2} = \left( \frac{x_{1} + x_{2}}{2}, \frac{y_{1} + y_{2}}{2} \right)$ when half distance. Now say that $\left( x_{n}, y_{n} \right)$ are the coordinates of the other mouse in $n – 1$ step:
$$
\begin{align*}
a_{1} &= \left( x_{1}, y_{1} \right)\\
a_{2} &= \left( \frac{x_{1} + x_{2}}{2}, \frac{y_{1} + y_{2}}{2} \right)\\
a_{3} &= \left( \frac{\frac{x_{1} + x_{2}}{2} + x_{3}}{2}, \frac{\frac{y_{1} + y_{2}}{2} + y_{3}}{2} \right)\\
&\dots\\
a_{n} &= \left( \frac{\frac{\frac{\frac{x_{1} + x_{2}}{2} + x_{3}}{2} + \ddots}{\ddots} + x_{n}}{2}, \frac{\frac{\frac{\frac{y_{1} + y_{2}}{2} + y_{3}}{2} + \ddots}{\ddots} + y_{n}}{2} \right)\\
\end{align*}
$$
So $\lim\limits_{n \to \infty}\left[ a_{n} \right] = 0$. The whole thing is the same for each step for any distance with small changes in the formula, but the appearance changes only minimally.
If we do this for all points, we could represent the distance between the points as infinite continued fractions, but that's not exactly what I want.
Try with Polar Coordinates
You could also try the pursuit curve to determine which describes the positions of the mise in space:
Let's say $r_{m}$ is the perimeter of the polygon in at $m$. If we form the gradient of one of the lines we are looking for into a subwhirl, we get $\Delta = \frac{r \cdot \sin\left( \theta + \frac{2 \cdot \pi}{n} \right) – r \cdot \sin\left( \theta \right)}{r \cdot \cos\left( \theta + \frac{2 \cdot \pi}{n} \right) – r \cdot \cos\left( \theta \right)} = \frac{\left( \cos\left( \frac{2 \cdot \pi}{n} \right) – 1 \right) \cdot \sin\left( \theta \right) + \sin\left( \frac{2 \cdot \pi}{n} \right) \cdot \cos\left( \theta \right)}{\left( \cos\left( \frac{2 \cdot \pi}{n} \right) – 1 \right) \cdot \cos\left( \theta \right) – \sin\left( \frac{2 \cdot \pi}{n} \right) \cdot \sin\left( \theta \right)}$. For this we assume that the polygons have been wired for $y$-axis symmetry.
Since they move the mice on their respective pursuit curve, the following applies: "The slope of the line is also equal to the derivative of the pursuit curve." aka:
$$
\begin{align*}
\frac{\operatorname{d}y}{\operatorname{d}x} &= \frac{r' \cdot \sin\left( \theta \right) + r \cdot \sin'\left( \theta \right)}{r' \cdot \cos\left( \theta \right) + r \cdot \cos'\left( \theta \right)}\\
\frac{\operatorname{d}y}{\operatorname{d}x} &= \frac{\cos\left( \theta \right)\, \operatorname{d}\theta + \sin\left( \theta \right)\, \operatorname{d}r}{\cos\left( \theta \right)\, \operatorname{d}r – \sin\left( \theta \right)\, \operatorname{d}\theta}\\
\end{align*}
$$
Both equations describe the same thing aka $\Delta = \frac{\operatorname{d}y}{\operatorname{d}x}$ applies, which means that:
$$
\begin{align*}
\Delta &= \frac{\operatorname{d}y}{\operatorname{d}x}\\
\frac{\left( \cos\left( \frac{2 \cdot \pi}{n} \right) – 1 \right) \cdot \sin\left( \theta \right) + \sin\left( \frac{2 \cdot \pi}{n} \right) \cdot \cos\left( \theta \right)}{\left( \cos\left( \frac{2 \cdot \pi}{n} \right) – 1 \right) \cdot \cos\left( \theta \right) – \sin\left( \frac{2 \cdot \pi}{n} \right) \cdot \sin\left( \theta \right)} &= \frac{\cos\left( \theta \right)\, \operatorname{d}\theta + \sin\left( \theta \right)\, \operatorname{d}r}{\cos\left( \theta \right)\, \operatorname{d}r – \sin\left( \theta \right)\, \operatorname{d}\theta}\\
\end{align*}
$$
Wolfram|Alpha simplifies the whole thing to $\sin\left( \frac{2 \cdot \pi}{n} \right) \cdot \frac{1}{r}\, \operatorname{d}r = \left( \cos\left( \frac{2 \cdot \pi}{n} \right) – 1 \right)\, \operatorname{d}\theta$ aka we'll get (assuming $r \in \mathbb{R}^{+})$:
$$
\begin{align*}
\sin\left( \frac{2 \cdot \pi}{n} \right) \cdot \frac{1}{r}\, \operatorname{d}r &= \left( \cos\left( \frac{2 \cdot \pi}{n} \right) – 1 \right)\, \operatorname{d}\theta\\
\int \sin\left( \frac{2 \cdot \pi}{n} \right) \cdot \frac{1}{r}\, \operatorname{d}r &= \int \left( \cos\left( \frac{2 \cdot \pi}{n} \right) – 1 \right)\, \operatorname{d}\theta\\
\sin\left( \frac{2 \cdot \pi}{n} \right) \cdot \int \frac{1}{r}\, \operatorname{d}r &= \left( \cos\left( \frac{2 \cdot \pi}{n} \right) – 1 \right) \cdot \theta + \text{cconstant}\\
\int \frac{1}{r}\, \operatorname{d}r &= \frac{\cos\left( \frac{2 \cdot \pi}{n} \right) – 1}{\sin\left( \frac{2 \cdot \pi}{n} \right)} \cdot \theta + \text{constant}\\
\ln\left( r \right) &= \frac{\cos\left( \frac{2 \cdot \pi}{n} \right) – 1}{\sin\left( \frac{2 \cdot \pi}{n} \right)} \cdot \theta + \text{constant}\\
r &= e^{\frac{\cos\left( \frac{2 \cdot \pi}{n} \right) – 1}{\sin\left( \frac{2 \cdot \pi}{n} \right)} \cdot \theta + \text{constant}}\\
\end{align*}
$$
We can determine the constant by the boundary condition that there are at least $3$ points lying on the unit circle. Let's just say that the curve $\left( 1,\, \frac{3 \cdot \pi}{2} – \frac{\pi}{n} \right)$ goes, then $\text{costant} \equiv \frac{\cos\left( \frac{2 \cdot \pi}{n} \right) – 1}{\sin\left( \frac{2 \cdot \pi}{n} \right)} \cdot \left( \frac{\pi}{n} – \frac{3 \cdot \pi}{2} \right)$ holds. We can now rotate the spiral arbitrarily by an angle $\theta_{0}$ in order to define it for the other mises and not for the $y$-axis symmetrical polygons:
$$\fbox{$
\begin{align*}
r &= e^{\frac{\cos\left( \frac{2 \cdot \pi}{n} \right) – 1}{\sin\left( \frac{2 \cdot \pi}{n} \right)} \cdot \left( \theta – \theta_{0} \right) + \frac{\cos\left( \frac{2 \cdot \pi}{n} \right) – 1}{\sin\left( \frac{2 \cdot \pi}{n} \right)} \cdot \left( \frac{\pi}{n} – \frac{3 \cdot \pi}{2} \right)}\\
\end{align*}
$}$$
Checking the formula for some examples like a rectangle seems to work aka I assume the formula is right:
However, I have some problems with the curve: Of course I could use it to determine the distances between the mise, but only as a function of the angle $\theta – \theta_{0}$ and not the distance. We could calculate the arc length from the angle, but the resulting integral seems a bit too complicated to me. In addition, I can't really understand the simplification that led to the result and I can't reconstruct it either…
But for the record:
$$
\begin{align*}
\operatorname{arc length}\left( \begin{matrix} t_{1}\\ t_{2}\\ \end{matrix};\, y\left( x \right) \right) &= \int\limits_{t_{1}}^{t_{2}} \sqrt{\operatorname{d}x + \operatorname{d}y}\, \operatorname{d}t\\
\operatorname{arc length}\left( \begin{matrix} t_{1}\\ t_{2}\\ \end{matrix};\, r\left( t \right) \right) &= \int\limits_{t_{1}}^{t_{2}} \sqrt{\left( \frac{\operatorname{d}r\left( t \right)}{\operatorname{d}t} \right)^{2} + \left( r\left( t \right) \right)^{2} \cdot \left( \frac{\operatorname{d}\theta\left( t \right)}{\operatorname{d}t} \right)^{2}}\, \operatorname{d}t\\
\operatorname{arc length}\left( \begin{matrix} \theta\left( t_{1} \right)\\ \theta\left( t_{2} \right)\\ \end{matrix};\, r\left( t \right) \right) &= \int\limits_{\theta\left( t_{1} \right)}^{\theta\left( t_{2} \right)} \sqrt{\left( \frac{\operatorname{d}r\left( \theta \right)}{\operatorname{d}\theta} \right)^{2} + \left( r\left( \theta \right) \right)^{2}}\, \operatorname{d}\theta\\
\end{align*}
$$


Best Answer
Suppose $n \geq 3$ mice are initially at the vertices of a regular $n$-sided polygon centered at the origin of the complex plane, with mouse 0 initially at point $1$ ($1+0i$). We can describe the position of mouse 0 as a function of time as
$$ z_0(t) = r(t) e^{i \theta(t)} $$
with $r(0)=1$ and $\theta(0)=0$. From here on I'll mostly abbreviate $z_0(t)$ as $z_0$, $r(t)$ as $r$, $\theta(t)$ as $\theta$, etc.
By symmetry, the mice will always be at the vertices of a regular $n$-sided polygon centered at the origin, so
$$ z_k = z_0 e^{2\pi k i/n} = r e^{i(\theta + 2\pi k/n)} $$
In particular, mouse 1 is at
$$ z_1 = z_0 e^{2\pi i/n} $$
So the direction from mouse 0 to mouse 1 is the same as the direction from the origin to
$$ z_1 - z_0 = (e^{2 \pi i/n} - 1) z_0 = e^{\pi i/n} (e^{\pi i/n} - e^{-\pi i/n}) = 2i e^{\pi i/n} \sin \left( \frac{\pi}{n} \right) z_0$$
Since mouse 0 moves with speed 1,
$$ \frac{dz_0}{dt} = \frac{z_1 - z_0}{|z_1-z_0|} = \frac{2i e^{\pi i/n} \sin \left(\frac{\pi}{n}\right)}{2 \sin \left(\frac{\pi}{n}\right)} \cdot \frac{z_0}{|z_0|} $$
$$ e^{i \theta} \frac{dr}{dt} + ir e^{i \theta} \frac{d\theta}{dt} = i e^{\pi i/n} \cdot e^{i\theta} $$
$$ \frac{dr}{dt} + ir \frac{d\theta}{dt} = i e^{\pi i/n} = i \cos \frac{\pi}{n} - \sin \frac{\pi}{n} $$
This complex equation must have its real and imaginary parts equal:
$$ \frac{dr}{dt} = -\sin \frac{\pi}{n} $$ $$ \frac{d\theta}{dt} = \frac{1}{r}\, \cos \frac{\pi}{n} $$
giving
$$ r(t) = 1 - t\sin \frac{\pi}{n} $$ for $0 \leq t < \csc \frac{\pi}{n}$, and
$$ \frac{d\theta}{dt} = \frac{\cos \frac{\pi}{n}}{1 - t \sin \frac{\pi}{n}} $$ $$ \theta(t) = - \left(\cot \frac{\pi}{n}\right) \ln\left(1-t \sin \frac{\pi}{n}\right) = - \left(\cot \frac{\pi}{n}\right) \ln r(t)$$
Since the speed is exactly 1, the arc length is the same as the time $t$.