The bounty for the best work out of Greg's answer, especially the
"solving for $\pi^*(x;q,a)$ in terms of all $\Pi^*$ functions (tedious but possible)"
part is over. Since Raymond's contributions might be very helpful to recall the necessary math, upvoting his answers is highly appreciated…I posted my attempt of a workout here. Comments welcome…
Original question:
I have two representations of $\pi(x)$:
-
The Prime Counting Function $\pi(x)$ is given
$$
\pi(x) = \operatorname{R}(x^1) – \sum_{\rho}\operatorname{R}(x^{\rho}) \tag{1}
$$
with $ \operatorname{R}(z) = \sum_{n=1}^{\infty} \frac{ \mu (n)}{n} \operatorname{li}(z^{1/n})$ and $\rho$ running over all the zeros of $\zeta$ function. -
This formula, while
widely believed to be correct, has not yet been proved.
$$
\pi(x) \approx \int\limits_2^x{\frac{dt}{\ln t}} – \frac{\sqrt x}{\ln x}\left( 1 + 2\sum_{\gamma} \ \ \frac{\sin(\gamma\ln x)}{\gamma}\right) \tag{2},
$$
with $\gamma=\text{Im}({\rho})$ being imaginary part of the roots of the $\zeta$ function.
Now I have two questions:
- Does the truth of $(2)$ depend on Riemann's Hypothesis or is it "just" what Wikipedia says, that The amplitude of the "noisy" part is heuristically about $\sqrt x/\ln x$?
- How to show the equivalence between $(1)$ and $(2)$? The integral logarithm is easily found in both representations, but how do the $\rho$-parts fit together? How do I get $\sin$s from $\text{li}(z^{1/n})$s? Does this invoke Gram's series:
$$
\operatorname{R}(z) = \sum_{n=1}^{\infty} \frac{ \mu (n)}{n} \operatorname{li}(z^{1/n}) = 1 + \sum_{k=1}^\infty \frac{(\ln z)^k}{k! k \zeta(k+1)} ?
$$
We can rewrite $\displaystyle \frac{\sin(\gamma\ln x)}{\gamma}=\frac{x^{i\gamma}-x^{-i\gamma}}{i\gamma}$ and I remember that I've seen a similar expression at Wikipedia:
$$
\psi_0(x) = x – \sum_\rho \frac{x^\rho}{\rho} – \ln 2\pi – \frac12 \ln(1-x^{-2}) ,
$$
But could this help, if at all? ($\psi_0(x)$ is the normalization of the Chebyshev function, see here)
Best Answer
Before answering to your question in the comment :
let's start with a sketch using von Mangoldt's derivation to obtain your equation $(1)$ that will be used for inspiration (for proofs see for example Edwards' chapter 3) :
Riemann's Explicit Formulas
The Euler product formula gives us : $$\tag{1}\boxed{\displaystyle\zeta(s)=\prod_{p\ \text{prime}}\frac 1{1-p^{-s}}}\quad\text{for}\ \ \Re(s)>1$$ so that $$\log \zeta(s)=-\sum_{p\ \text{prime}}\log(1-p^{-s})=\sum_p\sum_{k=1}^\infty \frac{p^{-ks}}k$$ minus the derivative will be : $$\tag{2}f(s):=-\frac{\zeta'(s)}{\zeta(s)}=\sum_p\sum_{k=1}^\infty \frac{\log\,p}{p^{ks}}=\sum_{n=1}^\infty \frac{\Lambda(n)}{n^s}\quad\text{for}\ \ \Re(s)>1$$ with $\Lambda$ the von Mangoldt function defined by $\ \Lambda(n):=\begin{cases} \log\, p & \text{if}\ n=p^k\ \text{and}\ k>0\\ 0 & \text{else} \end{cases}$
Let's use the definition of the second Chebyshev function : $\displaystyle \psi(x)=\sum_{n\leq x}\Lambda(n)$ and Abel's sum formula applied to $a(n):=\Lambda(n)$ and $\phi(n):=n^{-s}$ : $$\sum_{n=1}^\infty \frac{\Lambda(n)}{n^s}=s\int_1^\infty \frac {\sum_{n\leq x}\Lambda(n)}{x^{s+1}}\;dx$$ to rewrite $f(s)$ as (the lower bound became $0$ since $\phi(x)=0$ for $x<1$) : $$\tag{2.1}f(s)=s\int_0^{\infty}\frac{\psi(x)}{x^{s+1}}dx$$
But this is a Mellin transform which may be reverted to get Perron's formula (let's observe that the Dirichlet series $\displaystyle f(s)=\sum_{n=1}^\infty \frac{\Lambda(n)}{n^s}$ is absolutely convergent for $\Re(s)>1$ and suppose $c>1$) : $$\tag{3}\psi^*(x):=\frac1{2\pi i}\int_{c-i\infty}^{c+i\infty}f(s)\frac{x^s}s\,ds=\sum_{n=1}^\infty \Lambda(n) \frac1{2\pi i}\int_{c-i\infty}^{c+i\infty}\left(\frac xn\right)^s\frac{ds}s$$ This last integral may be evaluated using Fourier's theorem : $$\ \displaystyle\frac1{2\pi i}\int_{c-i\infty}^{c+i\infty}\frac{y^s}s ds= \begin{cases} \ \ 0 & 0<y<1\\ 1/2 & \quad y=1\\ \ \ 1 & \quad y>1\\ \end{cases}$$ and we obtain (as wished) that : $\displaystyle \tag{4}\psi^*(x)=\sum_{n\le x}^{*}\Lambda(n)$
with $\psi^*$ the second Chebyshev function except when $x$ is an integer because in this case the last term of the sum has to be divided by $2$. This will be the meaning of the $^*$ symbols in this article : at a first order discontinuity point (i.e. a jump) the result is the mean value of the limit at the left and the right.
Now $\psi^*(x)$ may also be written as : $$\tag{5}\psi^*(x)=-\frac1{2\pi i}\int_{c-i\infty}^{c+i\infty}\frac{\zeta'(s)}{\zeta(s)}\frac{x^s}s\,ds$$ Here the idea is simply to sum the residues of (all) the poles at the left of the vertical line of integration ($c>1$) at least if $x>1$ (for $0<x<1$ we would have to take the poles at the right and obtain $0$). These poles come from the denominator $s$, the pole of $\zeta$ at $1$ and the zeros with the correspondence : $0\mapsto -\frac{\zeta'(0)}{\zeta(0)},\ 1\mapsto x^1,\ \rho\mapsto -\frac{x^\rho}{\rho}$ for $\rho$ any zero of $\zeta\,$ (from the Weierstrass factorization of the Hadamard product) so that : $$\tag{6}\boxed{\displaystyle\psi^*(x)=x-\sum_{\rho} \frac {x^{\rho}}{\rho}-\frac{\zeta'(0)}{\zeta(0)}},\quad(x>1)$$ (in this post we won't distinguish the trivial from the non-trivial zeros $\rho$ ; for convergence the non-trivial roots should be grouped by pairs and sorted by increasing $|\Im(\rho)|$)
The Riemann prime-counting function is defined by : \begin{align} \tag{7}\Pi^*(x):&=\sum_{p^k\le x}^{*}\frac 1k=\sum_{n\le x}^{*}\frac {\Lambda(n)}{\log\,n}\\ &=\sum_{n\le x}^{*} \Lambda(n)\left(\int_n^x \frac{dt}{t\,\log^2 t}+\frac 1{\log\,x}\right)\\ &=\int_2^x\frac{\psi^*(t)\ dt}{t\,\log^2 t}+\frac{\psi^*(x)}{\log \,x}\\ &\tag{8}=\int_2^x\frac{\psi^{*'}(t)\ dt}{\log\,t}\\ \end{align} But $\ \displaystyle\operatorname{li}(x)=\int_2^x \frac{dt}{\log\,t}\,$ (Riemann's variant of the logarithmic integral) verifies $\ \displaystyle\operatorname{li}(x^r)'=\frac{r\,x^{r-1}}{\log\ x^r}=\frac{x^{r-1}}{\log\,x}$ so that from $(6)$ : $$\tag{9}\boxed{\displaystyle\Pi^*(x)=\operatorname{li}(x)-\sum_{\rho} \operatorname{li}(x^{\rho})},\quad(x>1)$$
The prime-counting function is defined by $\ \displaystyle\pi^*(x):=\sum_{p\le x}^{*}1\ $ while $\ \displaystyle\Pi^*(x):=\sum_{p^k\le x}^{*}\frac 1k$ will be : $$\tag{10}\Pi^*(x)=\sum_{k>0} \frac{\pi^{*}\bigl(x^{1/k}\bigr)}k$$ Applying the Möbius inversion formula $\ \displaystyle\pi^{*}(x):=\sum_{n=1}^{\infty} \frac{\mu(k)}k \Pi^*\bigl(x^{1/k}\bigr)\ $ to $(9)$ we get (with questionable convergence...) : $$\tag{11}\boxed{\displaystyle\pi^*(x)=R(x)-\sum_{\rho} R(x^{\rho})},\quad(x>1)$$ Where Riemann's $\,\displaystyle R(x):=\sum_{n=1}^{\infty} \frac{\mu(k)}k \operatorname{li}\bigl(x^{1/k}\bigr)\,$ may be written as a Gram series.
Dirichlet's L-functions
We will try to repeat the previous derivations but with $\zeta$ replaced by the Dirichlet L-function $$L(s,\chi)=\sum_{k=1}^\infty\frac{\chi(k)}{k^s}$$
With $\chi$ a Dirichlet character we get following Euler product : $$\tag{1'}\boxed{\displaystyle L(s,\chi)=\prod_{p\ \text{prime}}\frac 1{1-\chi(p)p^{-s}}}\quad\text{for}\ \ \Re(s)>1$$ so that ($\chi$ is multiplicative implying $\chi(p)^k=\chi(p^k)$) : $$\log L(s,\chi)=-\sum_{p\ \text{prime}}\log(1-\chi(p)p^{-s})=\sum_p\sum_{k=1}^\infty \frac{\chi(p^k)p^{-ks}}k$$ minus the derivative relatively to $s$ will be : $$\tag{2'}f(s,\chi):=-\frac{L'(s,\chi)}{L(s,\chi)}=\sum_p\sum_{k=1}^\infty \frac{\chi(p^k)\log\,p}{p^{ks}}=\sum_{n=1}^\infty \frac{\chi(n)\Lambda(n)}{n^s}\quad\text{for}\ \ \Re(s)>1$$
The Perron formula applied to $f(s,\chi)$ gives : $$\tag{3'}\psi^*(x,\chi):=\frac1{2\pi i}\int_{c-i\infty}^{c+i\infty}f(s,\chi)\frac{x^s}s\,ds=\sum_{n=1}^\infty \chi(n)\Lambda(n) \frac1{2\pi i}\int_{c-i\infty}^{c+i\infty}\left(\frac xn\right)^s\frac{ds}s$$ $$\tag{4'}\psi^*(x,\chi)=\sum_{n\le x}^{*}\chi(n)\Lambda(n)$$
But $\psi^*(x,\chi)$ may also be written as : $$\tag{5'}\psi^*(x,\chi)=-\frac1{2\pi i}\int_{c-i\infty}^{c+i\infty}\frac{L'(s,\chi)}{L(s,\chi)}\frac{x^s}s\,ds$$ Again we compute the sum of the residues at (all) the poles to the left of the vertical line of integration (for $c>1$). The contributions from the different poles will be : $0\mapsto -\frac{L'(0,\chi)}{L(0,\chi)},\ \rho\mapsto -\frac{x^\rho}{\rho}$ for $\rho$ any zero of $L(s,\chi)\,$ (from Weierstrass factorization) so that : $$\tag{6'}\boxed{\displaystyle\psi^*(x,\chi)=-\sum_{\rho} \frac {x^{\rho}}{\rho}-\frac{L'(0,\chi)}{L(0,\chi)}},\quad(x>1)$$ (the sum over $\rho$ combines the trivial and the non-trivial zeros and we will suppose that $\chi$ is a non principal character so that $\,L(s,\chi)\,$ is regular everywhere, for a principal character we should add a $x$ contribution from the pole at $1$)
An analogue to the Riemann prime-counting function will be : \begin{align} \tag{7'}\Pi^*(x,\chi):&=\sum_{p^k\le x}^{*}\frac {\chi(p^k)}k=\sum_{n\le x}^{*}\frac {\chi(n)\Lambda(n)}{\log\,n}\\ &=\sum_{n\le x}^{*} \chi(n)\Lambda(n)\left(\int_n^x \frac{dt}{t\,\log^2 t}+\frac 1{\log\,x}\right)\\ &=\int_2^x\frac{\psi^*(t,\chi)\ dt}{t\,\log^2 t}+\frac{\psi^*(x,\chi)}{\log \,x}\\ &\tag{8'}=\int_2^x\frac{\psi^{*'}(t,\chi)\ dt}{\log\,t}\\ \end{align} From $\ \displaystyle\operatorname{li}(x^r)'=\frac{x^{r-1}}{\log\,x}$ and $(6')$ we get : $$\tag{9'}\boxed{\displaystyle\Pi^*(x,\chi)=-\sum_{\rho} \operatorname{li}(x^{\rho})},\quad(x>1)$$ (for $\chi$ a principal character there is an additional $\,\operatorname{li}(x)$ term)
The $\chi$-prime-counting function is $\ \displaystyle\pi^*(x,\chi):=\sum_{p\le x}^{*}\chi(p) $ while $\ \displaystyle\Pi^*(x,\chi):=\sum_{p^k\le x}^{*}\frac {\chi(p^k)}k$ so that : $$\tag{10'}\Pi^*(x,\chi)=\sum_{k>0} \frac{\pi^{*}\bigl(x^{1/k},\chi^k\bigr)}k,\quad(x>1)$$
Broken analogy...
The problem here is that we have $\,\pi^{*}\bigl(x^{1/k},\chi^k\bigr)$ in the sum and not $\,\pi^{*}\bigl(x^{1/k},\chi\bigr)$.
For principal characters (when $\,\chi(p)=0$ or $1$ so that $\,\chi^k(p)=\chi(p)\,$ for $k$ positive) we may apply the Möbius inversion formula to $(9')$ and get : $$\tag{11'}\displaystyle\pi^*(x,\chi)=[R(x)]-\sum_{\rho} R(x^{\rho})$$ (since $\chi$ is a principal character we must add the $R(x)$ term from the pole at $1$)
but this doesn't work in general and the equality becomes questionable after the first prime $p$ such that $\,\chi^k(p)\not =\chi(p)\,$ as we will see by considering your specific question.
We want $\chi$ to be the Dirichlet character modulo $4$ ($\chi_2$ in the link) defined by $\ \displaystyle\chi(0)=0,\ \chi(1)=1,\ \chi(2)=0,\ \chi(3)=-1\ $ and get : $$\tag{12'}L(s,\chi)=\sum_{n=0}^\infty\frac {(-1)^n}{(2n+1)^s}=\beta(s)$$ with $\beta$ the Dirichlet beta function we could hope that : $$\pi^*(x,\chi)=\displaystyle\pi_{4,1}^*(x)-\pi_{4,3}^*(x)\approx -\sum_{\rho} R(x^{\rho})$$ with $\pi_{q,a}(x)=\#\{p:p\ \text{is prime and}\ \,p\le x\,\ \text{and}\ \,p\equiv a\pmod q\}$
But, from $(10')$ and $(9')$, we have in fact : \begin{align} \Pi^*(x,\chi)&=\sum_{k>0} \frac{\pi_{4,1}^{*}\bigl(x^{1/k}\bigr)+(-1)^k\,\pi_{4,3}^{*}\bigl(x^{1/k}\bigr)}k=-\sum_{\rho} \operatorname{li}(x^{\rho})\\ &=\sum_{k>0} \frac{\pi_{4,1}^{*}\bigl(x^{1/k}\bigr)-\,\pi_{4,3}^{*}\bigl(x^{1/k}\bigr)}k+2\sum_{j>0} \frac{\pi_{4,3}^{*}\left(\sqrt{x}^{1/j}\right)}{2j}\\ \end{align} so that the Möbius transformation will return the exact (with $\rho$ any zero of $\beta$) : $$\tag{13'}\boxed{\displaystyle\pi_{4,1}^{*}(x)-\pi_{4,3}^{*}(x)+\pi_{4,3}^{*}\left(\sqrt{x}\right)=-\sum_{\rho} R(x^{\rho})}$$
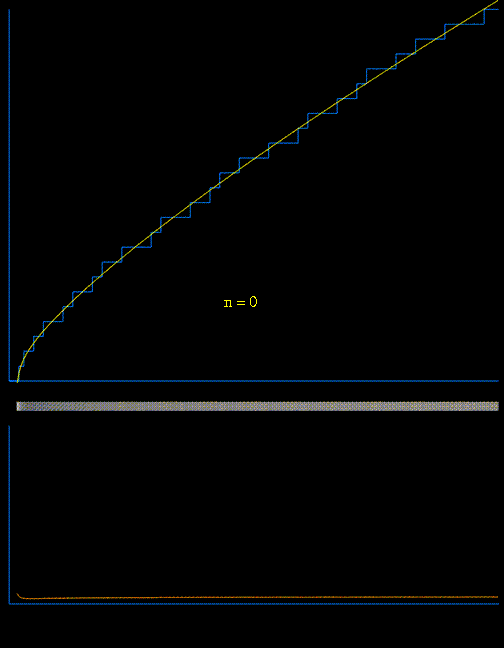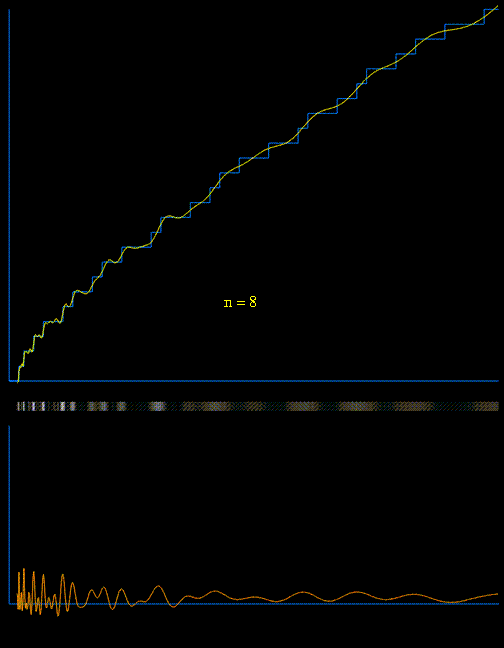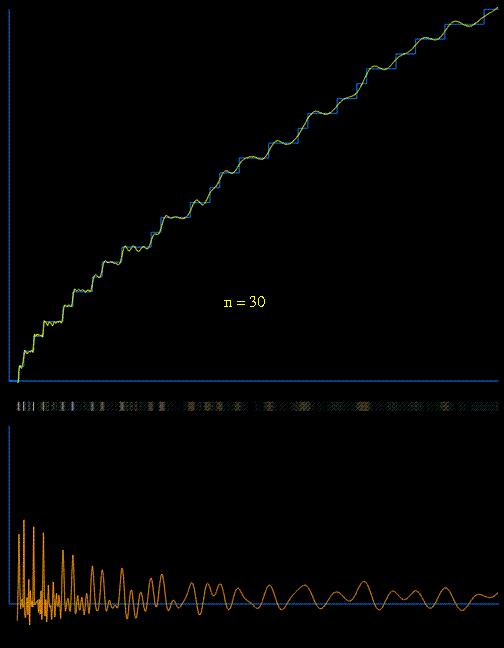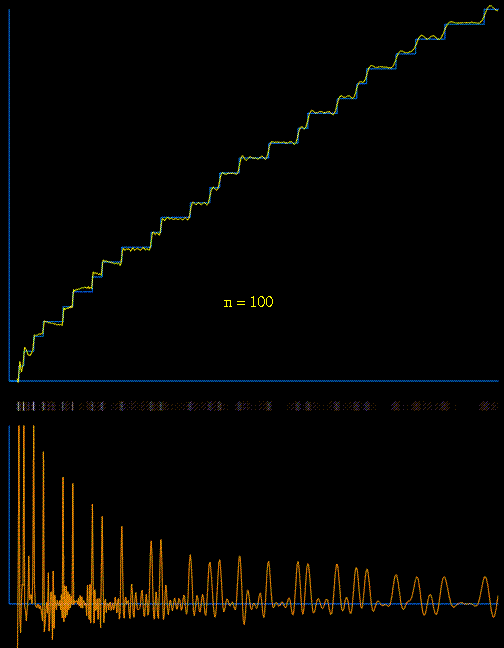
To show the effect of the $\,\pi_{4,3}^{*}\left(\sqrt{x}\right)\,$ term let's exhibit an approximation of the expression at the right (taking the $40$ first terms of the sum $R$ and the $300$ first non-trivial zeros of the Dirichlet-beta function) that we compare to the exact (dark) result for $\,\pi^*(x,\chi)=\displaystyle\pi_{4,1}^*(x)-\pi_{4,3}^*(x)\,$ in the interval $\,[5,80]$ :
The initial behavior seems right : $-1$ at $3$ followed by $+1$ at $5$ and $-1$ at $7$ but just after that there is a first 'irregularity' at $9=3^2$ because $\chi(3^2)=1$ while $\chi(3)=-1$. After that the behavior is correct (shifted $+1$ of course) until another irregularity at $49=7^2$ again because $\chi(7^2)=1$. The next one will be at $121=11^2$ and at all the following squares of primes of gender $4n+3$...
ADDITION: Draks telescoping
The situation was blocked at this point until draks, using a suggestion of Greg Martin, proposed in february his powerful telescoping method to obtain (the $\rho_\zeta$ and $\rho_\beta$ are respectively all the zeros of the $\zeta$ and $\beta$ function) : $$\tag{14'}\pi_{4,3}(x):=\sum_{k=0}^\infty\;2^{-k-1}\left( R\left(x^{1/2^{k}}\right)-\sum_{\rho_\zeta} R\left(x^{\rho_\zeta/2^k}\right) +\sum_{\rho_\beta} R\left(x^{\rho_\beta/2^k}\right) \right)$$
We may obtain this result too (with a minor correction) by rewriting $(11)$ as (for $x>2$) : $$\pi^*(x)=1+\pi_{4,1}^{*}(x)+\pi_{4,3}^{*}(x)=R(x)-\sum_{\rho_\zeta} R(x^{\rho_\zeta})$$ ($1$ was added since all primes except $2$ are equal to $1$ or $3\bmod{4}$) and using $(13')$ : $$\pi_{4,1}^{*}(x)-\pi_{4,3}^{*}(x)+\pi_{4,3}^{*}\left(\sqrt{x}\right)=-\sum_{\rho_\beta} R(x^{\rho_\beta})$$ Subtracting these equations gives : $$2\pi_{4,3}^{*}(x)-\pi_{4,3}^{*}\left(\sqrt{x}\right)=R(x)-1-\sum_{\rho_\zeta} R(x^{\rho_\zeta})+\sum_{\rho_\beta} R(x^{\rho_\beta})$$ while draks' telescoping sum $\ \displaystyle\frac 12\sum_{k=0}^\infty \frac{f\left(x^{1/2^{k}}\right)}{2^k}$ is : $$\sum_{k=0}^\infty \frac {2\,\pi_{4,3}^{*}(x^{1/2^{k}})-\pi_{4,3}^{*}\bigl(x^{1/2^{k+1}}\bigr)}{2^{k+1}}=\sum_{k=0}^\infty \frac {R\left(x^{1/2^{k}}\right)-1-\sum_{\rho_\zeta} R\left(x^{\rho_\zeta/2^k}\right)+\sum_{\rho_\beta} R\left(x^{\rho_\beta/2^k}\right)}{2^{k+1}}$$ producing draks' formula : $$\tag{15'}\boxed{\displaystyle\pi_{4,3}^{*}(x)=\sum_{k=0}^\infty \frac {R\left(x^{1/2^{k}}\right)-\sum_{\rho_\zeta} R\left(x^{\rho_\zeta/2^k}\right)+\sum_{\rho_\beta} R\left(x^{\rho_\beta/2^k}\right)}{2^{k+1}}-1}$$ A similar formula may be written for $\pi_{4,1}$ and this answers positively the initial question !
Let's finish with a plot of $\pi_{4,3}^{*}(x)$ from $4$ to $100$ (more details here with the pari/gp scripts used)