Werner Boy's Surface (with a Hole)
A really nice way to represent it is Boy's Surface with a hole poked in it.
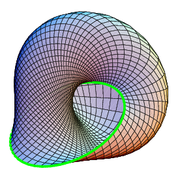
Boy's surface is an immersion of the 2-dimensional projective plane $P$ into Euclidean $\Bbb R^3$. It's not an embedding because it has self-intersections and a triple point. But it's smooth everywhere and has no pinches or creases or cusps.
Now $P=M+D$ where $M$ is a Möbius band and $D$ is a disk, i.e. gluing $D$ and $M$ together gives $P$. The other way round, poking a hole (removing $D$) from $P$ will yield $M$. Notice that we can pick to remove a disc that does not intersect with the remaining $M$.
The page above has images of a sculpture in Oberwolfach, which is specially nice because it is minimizing Willmore energy using Bryant-Kusner-parametrization. Removing the top dome would leave a Möbius band with a flat circle as its boundary.

And there are also nice animations, cf. youtube: Boy's surface.
Great David Hilbert conjectured that no such immersion exists, but Werner Boy proved him wrong.
Möbius Snail
A different representation with circular boundary is the "Sudanese Möbius strip" which has no self-intersections. An image and description are here.
Adding a disc in order to complete it to the projective plane will introduce self-intersections and creases, though, i.e. places where the surface is not smooth. More renderings are here.

Möbius Wheel (from Boy's Surface)
Returning to Boy's surface, here are some renderings of a Möbius strip with (almost) circular boundary: W1,
W2,
W3,
W4. These renderings were created by changing the Bryant-Kusner parametrization in such a way that only a part is rendered (which effectively pokes a hole) and by pulling the boundary of the resulting Möbius strip to the equatorial plane. The resulting shape has $D_{2\cdot 3}$ dihedral symmetry with a triple-point in the center. There is a detailed description.




All images from Wikipedia / Wikimedia Commons.







Best Answer
They are homeomorphic, and they are both orientable.
It’s not clear whether you’re considering just the surfaces of these objects, or the whole solid objects, but in either case, the answer is the same. I’ll assume in the following that you mean the surfaces, but it adapts straightforwardly to the solid bodies as well. I’m leaving a lot of details out here; if you would like me to elaborate on anything, let me know.
To get the homeomorphism, first pick nice parametrisations of the torus and the fattened Möbius band. $\newcommand{\x}{\mathbf{x}}\newcommand{\y}{\mathbf{y}}\newcommand{\R}{\mathbb{R}}$The torus can be parametrised by pairs $(\theta,\x)$, where $\theta \in [0,2 \pi)$, and $\x \in \R^2$, $|\x| = 1$, i.e. $x$ is a point on the standard unit circle. Here $\theta$ represents the “major” angle, i.e. the angle on the large-diameter circle round the origin, and $\x$ represents the point on the small-diameter circle.
The fattened band is exactly the same idea, but a little tricker to write down. Let $Q_\theta$, for $\theta \in [0,2\pi]$, be the unit square in $\R^2$ rotated by $\theta/4$ radians. So as $\theta$ varies from $0$ to $2\pi$, $Q_\theta$ rotates by a quarter-turn, and ends up back where it started. Now the fattened band can be parametrised by pairs $(\theta,y)$, where $y \in Q_\theta$.
Now one direction of the homemorphism, from the band to the torus, is described easily by sending $(\theta,\y)$ to $(\theta, \frac{\y}{|\y|})$.
Once one has the homeomorphism, it follows that since the torus is orientable, so is the fattened Möbius band.
One take-home here is the Möbius band is very different from the fattened Möbius band; the non-orientability of the former doesn’t imply anything about the latter.