What is the third order term in the Taylor Series Expansion? I know it will just be third order partial derivatives but I want to know how is it expressed in a compact Matrix notation. For instance Jacobian for first order, Hessian for second order partial derivatives.
In other words, what is the third order term in the equation below? Thanks for your help!
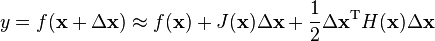
Best Answer
Well, $f: \mathbb{R}^n \rightarrow \mathbb{R}^n$ has multivariate Taylor expansion at $x+h$ centered at $x$ of: $$ f(x+h) = f(x)+\sum_{i=1}^n \frac{\partial f}{\partial x_i}h_i +\frac{1}{2}\sum_{i,j=1}^n \frac{\partial^2 f}{\partial x_i\partial x_j}h_ih_j+\frac{1}{6}\sum_{i,j,k=1}^n \frac{\partial^3 f}{\partial x_i\partial x_j\partial x_k}h_ih_jh_k+ \cdots$$ Here we could define $T: \mathbb{R}^n \times \mathbb{R}^n \times \mathbb{R}^n \rightarrow \mathbb{R}^n $ by its values on the basis elements $e_i,e_j,e_k$ (unit-vector basis for Cartesian coordinates in $n$-dimensions) $$ T_{ijk}=\sum_{i,j,k=1}^n \frac{\partial^3 f}{\partial x_i\partial x_j\partial x_k} $$ The question is, can we write the formula $\sum_{i,j,k=1}^nT_{ijk}h_ih_jh_k$ as a matrix multiplication of some sort... I suggest we consider $\mathbb{R}$-valued $f$ as a starting point.
(with the proper conventions set forth there is a way to write this as a matrix multiplication, but, I think in the process of doing such we lose track of the manifest trilinearity, I'm not well-versed in the needed notation at this point in time so I'll leave my answer here as it stands since expressing this as a matrix multiplication on an abstract space is not that interesting, well, at least to me today)