Wikipedia's section on rigid shapes does not appear to actually define what a rigid shape is. Rather it defines 'same shape' and 'rigid transformations' without giving any definitions of what is necessary and sufficient for a shape to be considered rigid.
For instance, I've seen the following image:
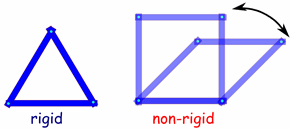
I understand intuitively why the triangle is rigid and quadrilateral is non-rigid. It is also my understanding that inserting a single diagonal connection into the quadrilateral would make the shape rigid? However, given the following image (labeling the shapes $S_1$, $S_2$ and $S_3$ in sequence left to right):

If $S_1$ had a single diagonal connection AB, it would be possible to flip ADB over axis q to obtain a shape similar to $S_2$ with the addition of connection AB (my explanation may not be the greatest). This shape is clearly not the same as $S_1$, so how can we say $S_1$ with a single diagonal connection CD is rigid? I feel I am unclear on what the definition of rigidity actually is.
Best Answer
Although the accepted answer by rschwieb is an excellent one, I think there is a connection between the mathematical notion of "rigid motion" and the physical notion of "structural rigidity" that has not been mentioned yet.
Let us define a diagram to refer to any finite collection of line segments with labeled endpoints in the plane. Suppose we have two kinds of data about a given diagram: its incidence relations (i.e. knowing which points are the endpoints of which which line segments) and its linear measurements (i.e. knowing how long the segments are). We ask the question:
Another (slightly less formal) way to put this is: If you know how long all the segments in a diagram are, can you draw the diagram?
First, let's notice that at best we might be able to say that a diagram is completely specified up to a rigid motion. That is, even if could reconstruct a diagram from its incidence relations and linear measurements, we would not know where to position it in the plane or how to orient it, because a rigid motion of the plane preserves all incidence and metric properties while possibly changing position and orientation.
But a more significant observation is that knowing the incidence relations and linear measurements of a diagram does not, in general, completely specify a diagram. To see this, just look at the example in the OP of a "nonrigid" shape: A square that deforms into a rhombus. The original diagram (the square) and the deformed diagram (the rhombus) have exactly the same incidence relationships and linear measurements, but the angles in them are different.
We can take this as a mathematical characterization of the physical notion of "structural rigidity": If a diagram is completely determined (up to a rigid motion) by its incidence relations and its linear measurements, we can call it a rigid diagram.
Now consider a triangle. Suppose we know the three side-lengths of a given triangle $\Delta ABC$. Is it possible to reconstruct everything else about the triangle?
The answer is Yes. This is known as the Side-Side-Side property. In high school geometry it is usually formulated as a criterion for proving that two triangles are congruent:
The Side-Side-Side property tells you that if the sides of a triangle are non-deformable then its angles are completely "locked in", i.e. the entire triangle is rigid.
Note that this is not true for any polygon other than a triangle: There is no such thing as a "Side-Side-Side-Side" congruence criterion for quadrilaterals.
Now let's consider the examples in the OP. The diagram $S_1$, without the dotted diagonals, is a quadrilateral $ADBC$. Such a quadrilateral is not rigid, because one can draw another quadrilateral $A'D'B'C'$ with all corresponding lengths exactly the same but with different interior angles.
However, if you add even one of the dotted segments (for example, $\overline{DC}$) into the diagram, then the diagram would be rigid, because the triangles $\Delta ADC$ and $\Delta BDC$ are rigid.
Exactly the same remarks apply to $S_2$.
For $S_3$, the question of whether or not the diagram is rigid depends on whether the line that appears to join $A$ to $C$ and the line that appears to join $B$ to $D$ is actually a segment, and if so whether the point that appears to be at the intersection of those segments (call it $P$) is explicitly part of the diagram or not, and whether $\overline{AP}$, $\overline{PC}$, etc. are all part of the diagram. (Notice that this is all contained in the "incidence relations" specification of a diagram.) If they are, then the diagram is rigid; otherwise, it is just a non-rigid quadrilateral.