A few months ago, when I was studying strategies for the evaluation of functional programs, I found that the optimal algorithm uses something called Interaction Combinators, a graph system based on a few nodes and rewrite rules.

I've implemented and got some surprising results with it. I tried learning more, only to realize there are very few papers and almost nobody talking about it. Another day, by sheer luck, I stumble with this paper about chemical computers that would be "the future of computation". Midway through my read, I see this:

The similarity to Interaction Nets in striking. The nodes, the rules, the principal ports – on its core, the system is mostly the same. I tried looking at references to find more about "it", but didn't find anything very relevant, so I gave up. Another day, by sheer luck once again, I sumble with this blog post about some kind of graphical linear algebra that "can divide by zero". Midway through the read, I see this:
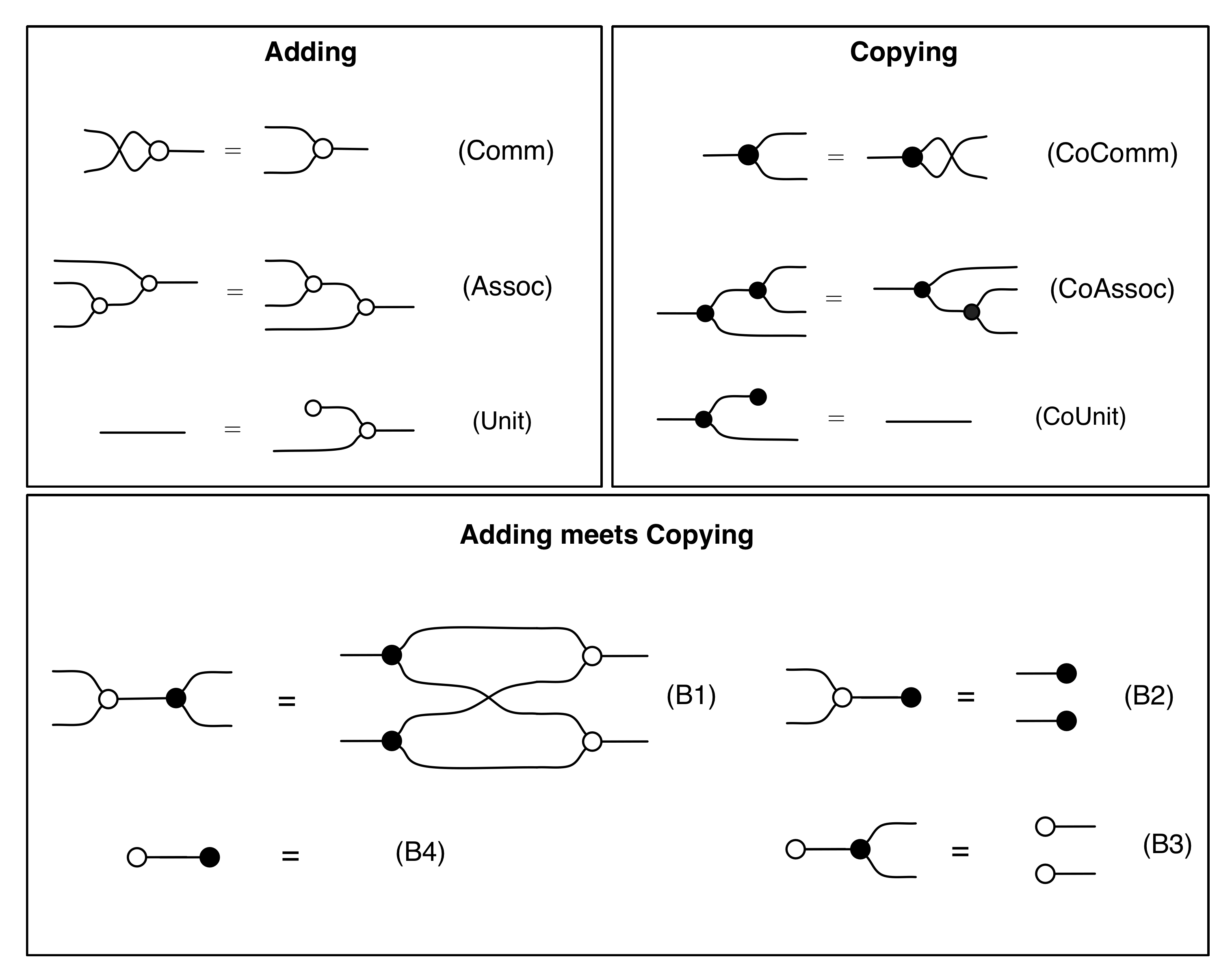
Once again, the same "thing" can be seen. There are some minor differences but, on its core, it is the same. What is that thing in common with those systems? How is it called, what is its importance, where is it studied and, most importantly, why it keeps showing in completely different fields?
Best Answer
First, this is not the only spot where bizarre squiggly lines are used to represent deep concepts. There are things such as Feynmann diagrams,
circuit diagrams,
Petri nets,
and others. So this isn't the only spot where this type of thing is used. These things are called string diagrams and were first used by Roger Penrose in Combinatorial Mathematics and its Applications and Spinors and Spacetime for calculating with tensors.
The concept uses Poincaré duality to represent structures of dimension $d$ by structures of dimension 2-$d$. Objects are represented by portions of a plane, a 1-cell is represented by a vertical segment (or string) separating the plane into two, and a 2-cell is represented by an intersection of strings. Monoidal categories can be pictured this way, and the graphical language may be extended to represent expressions in categories with other structures, such as symmetric monoidal categories, and dagger categories.
Hope this helps!
References:
These are a few sites/papers that have good information (and good citations) about this topic; I'll be adding more as I find them: