Paul Erdős said this about the $3n + 1$ conjecture:
Mathematics may not be ready for such problems.
Similarly, there are parts of mathematics that I am not yet ready for. Some things, however, I might never be ready for in this life. They must be reserved then to the afterlife.
Assume that we enter a paradise, then it's finally time to waste time on some mathematics that are both beautiful and useless, and I have been collecting those little gems but I want more, so I am asking you to provide more examples.
I should explain what is beautiful and what is useless. Mathematical beauty is rather subjective, and I won't try to define it precisely, but it should be easily stated, and has "surprising complexity", and should not have many arbitrary rules like chess.
Useless means that it is not only useless to a non-mathematician, it's also useless to other parts of mathematics. Some subjects in mathematics, like category theory, are useful mainly for their relation to other fields of mathematics.
This isn't just about unsolved problems, but also about solved and polished areas of mathematics that nevertheless are beautiful yet isolated from the other parts of mathematics.
I'll give some examples. Note that a lot of them have a distinct geometric flavor, this is because I am a geometer in heart and hoof, and I'm kinda sad that there isn't beautiful geometry that's both useful and innovative anymore. It seems all the good work in beautiful and useful geometry has been done by Newton et al.
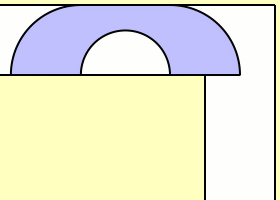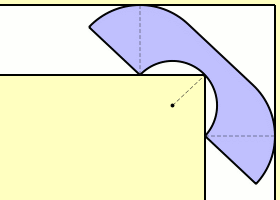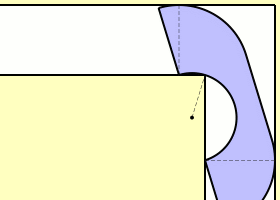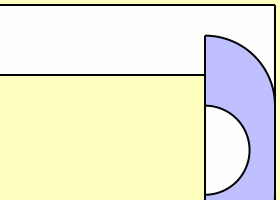
The moving sofa problem
What is the largest area of a sofa that can be moved through a corner like this?
Lebesgue's universal covering problem
As explained in this math stackexchange question, the following question is easy to state and visualize, but hard to solve:
Let "set" denote any subset of the Euclidean plane. What is the greatest lower bound of the diameter of any set which contains a subset congruent to every set of diameter 1?
… progress on this question, which has been painfully slow in the past, may be even more painfully slow in the future.
and John Baez, who wrote some blog posts on this problem, commented
My whole interest in this problem is rather morbid, I don’t know any reason that it’s important. I don’t see it as connected to lots of other beautiful math. It just seems astoundingly hard compared to what you might initially think. I admire people who work on it in the same way I admire people who decide to ski across the Antarctic… As far as the math goes, it’s just high-school geometry. But it’s carried to a fanatical level of intensity.
Computational hardness results
A lot of amusing game-like things are computationally hard, for example, Tetris, some Nintendo games, paper folding, etc. Proving these are amusing but useless.
Minimal axioms for Boolean algebra
Basically, code golf for Boolean algebras.
The same game can be played for other kinds of algebraic systems, of course, but the Boolean algebra is the most heavily studied so far. George Grätzer's books on Lattice Theory seems to contain a lot about this.
Somebody who worked on this problem in this life, instead of the afterlife, is Carew Meredith, who found this gnarly beast of an axiom:
$$ ( ( ( ( ( \phi \to \psi ) \to ( \neg \chi \to \neg \theta )
) \to \chi ) \to \tau ) \to (
( \tau \to \phi ) \to ( \theta \to \phi )
) )
$$
An obscure Irish lecturer, Meredith (1904-1976) became enamored with logic somewhat late in life after attending talks by Lukasiewicz and produced many remarkable results such as this axiom. From his obituary: "He did logic whenever time and opportunity presented themselves, and he did it on whatever materials came to hand: in a pub, his favored pint of porter within reach, he would use the inside of cigarette packs to write proofs for logical colleagues."
Tabulate properties of high-dimensional symmetries
2- and 3- dimensional symmetries have too many applications to list, but high-dimensional symmetries is mostly for beautiful, useless fun.
Symmetry groups in high dimensions have been quite intensively studied, with a lot of intricate tables of their properties made. Just looking at them makes me want to waste a few year understanding and verifying them.
And omc I would totally spend years just playing zometools…

Pretty much all of modern set theory
I used to think that every true mathematician knows how to show the Continuum Hypothesis is independent of ZFC, then I realized that most don't because it's a waste of their time to learn forcing.
I have read some posts by Asaf Karagila and Joel David Hamkins. The things that modern set theorists do seem like a very carefully justified insanity, the best modern analogue of medieval scholastic philosophy.
I mean, look at these hierarchical things they put. That's the nine levels of angels and devils. Figure can be seen on the cover of Akihito Kanamori's The Higher Infinite (the title is appropriately dramatic).

And I swear this could be a centerfold for The Pilgrim's Progress (to Cantor's Paradise). Figure from When zero is equal to one

Same can be said for model theory, computational complexity (what kind of irl computer would ever need to use a Turing jump, or infinite injury?), reverse mathematics (might be useful for more than just logic, need reference), hyperarithmetical theory, and a lot of other parts of mathematical logic, really.
Works by Paul Erdos
I admire his work greatly, but he just wrote so much and about so many fields I don't care about. Considering how much of his mathematics seems to be about the art of specific problem solving, I expect a lot of it to be useless beauties.
Same can be said for work by Gauss, Euler, Ramanujan, etc.
Weird constructions using straightedge and compass
The 65537-gon is constructible, and Johann Gustav Hermes made a construction back in 1894. He should have done something better with his life (since he wasn't in his afterlife yet).
And there are two theorems whose proofs are elementary, but don't worth the time to look at in this life. I have once had a glance at their proofs and they were some really delicate constructions.
Mohr–Mascheroni theorem states that any geometric construction that can be performed by a compass and straightedge can be performed by a compass alone.
Poncelet–Steiner theorem states that whatever can be constructed by straightedge and compass together can be constructed by straightedge alone, provided that a single circle and its centre are given. In 1904, Francesco Severi proved that any small arc together with the centre will suffice.
Many topics in knot/link theory
I recognize that knot theory has lots of applications, but a lot of it is really only for its own beauty.
Just a small list of things in knot/link theory: wild knots, hyperbolic volume, 4-dimensional braids, etc.
Dissections
There are many paradoxes of dissections, such as Banach-Tarski paradox, von Neumann paradox, Hausdorff paradox, Tarski's circle-squaring problem…
And problems of equidissection, such as the famed Monsky's theorem
A square can't be divided into an odd number of triangles with the same area.
The proof uses 2-adic numbers.
This summary shows why this is perfect for the afterlife:
Equidissections do not have many direct applications. They are considered interesting because the results are counterintuitive at first, and for a geometry problem with such a simple definition, the theory requires some surprisingly sophisticated algebraic tools. Many of the results rely upon extending p-adic valuations to the real numbers and extending Sperner's lemma to more general colored graphs.
Planar tiling, spatial honeycombs, and higher dimensional analogues
There are 15 known pentagonal tilings and these are probably all of them. A complete personal understanding would be nice but take too much time, and I can't think of a single application of this result to anywhere else in math.
The Voderberg tiling always seems cool to me, and it's almost miraculous how it could all fit together perfectly in a spiral pattern. I defer understanding the proof to the afterlife.
The einstein problem has some really bizarre bug-like solutions that look really cool, but are totally useless.

(I was going to put "Wang's Tiles" here, but then learned that they have applications in procedural synthesis)
Problems in packing things together really tightly
Again, I admit that some of these might have some applications, but mostly they seem to be done for pure amusement.
The dodecahedral theorem, the many many variations on sphere packing, packing circles in a circle, packing X in a Y, and so on.
Best Answer
This is very useless. It is basically the (fibrated) boundary of the intersection of eight $2$-spheres. It can be generalized to higher dimensions but remains to be useless in all of those dimensions.
However, assuming we enter paradise, I would absolutely go to town on this thing. I would explore the properties of this shape in all of their useless beauty...
...I would investigate it as a symplectic object and study torsion on it. I would study it as a more rigid object using a non-contractible riemannian metric. I would do analysis on the force needed to crush this object and also study metric decay as the geometry becomes more and more random. I would study it as a network. I would study spaces where this object is a point in that space. I would also investigate every topological and algebraic property of the object. Lastly, I would explore the dynaimcs of an algebraic space in which this object is a point and the points "spin" via different moments, like an electron and I'd study and classify all the force mediating "particles" in said space. I would study a lot more about this object but time is money.