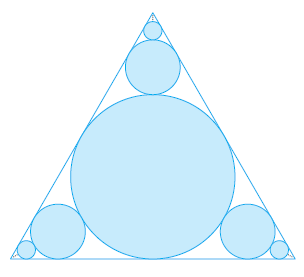
In the figure there are infinitely many circles approaching the vertices of an equilateral triangle, each circle touching other circles and sides of the triangle. If the triangle has sides of length 1, find the total area occupied by the circles.
I need to find the total area of the circles.
I know this is going to have something to do with summation as a value approaches infinity, but I'm not entirely sure how to approach the problem. Here's what I have so far:
I know that the radius of the central inscribed circle is $ \frac{\sqrt{3}}{6} $. As such, the area of the first circle is $$ A = \pi\left(\frac{\sqrt{3}}{6}\right)^2. $$ Because there are three "branches" of infinite circles, I'm assuming that the answer will look something like: $$ A = \pi\left(\frac{\sqrt{3}}{6}\right)^2 + 3 \sum_{1}^{\infty}\text{something}.$$

Best Answer
Look at the following figure carefully,
As the triangle is equilateral ($AC$ is the angle bisector). So, $\angle ACD = 30^{\circ}$ $$\tan 30^{\circ} = \frac{AD}{DC} = 2AD\ (\because DC = 1/2) $$ $$\therefore AD = \frac{1}{2\sqrt{3}}$$ This is the radius of the bigger circle, let its area be $A_1$ $$\therefore A_1 = \frac{\pi}{12}$$
To calculate the radius of the next smaller circle (let it be $x$), please note that
$$AC = \frac{1}{\sqrt{3}}$$
$$AB =\frac{1}{2\sqrt{3}} +x$$
$$\therefore BC = AC - AB =\frac{1}{2\sqrt{3}} -x $$
Note that triangles $ADC$ and $BCE$ are similar. $$\therefore \frac{AD}{AC} = \frac{BE}{BC}$$
$$\frac{1}{2\sqrt{3}} \times \sqrt{3} = x \times \left( \frac{2\sqrt{3}}{1-2\sqrt{3}x} \right)$$
$$\therefore x = \frac{1}{6\sqrt{3}}$$
Similarly we can find the radii of the next circles. They would be $\frac{1}{18\sqrt{3}}$, $\frac{1}{54\sqrt{3}}, ...$
Now, the main answer,
The sequence $\frac{1}{6\sqrt{3}},\frac{1}{18\sqrt{3}}, \frac{1}{54\sqrt{3}}, ... $ can be generally written as $\frac{1}{6\sqrt{3}(3)^{n-1}}$
Total area of these circles,
$$T = \frac{\pi}{12} + 3\sum_{n=1}^{\infty} \pi {\left(\frac{1}{6\sqrt{3}(3)^{n-1}} \right)}^2 $$
Notice that, $$\sum_{n=1}^{\infty} \pi {\left(\frac{1}{6\sqrt{3}(3)^{n-1}}\right)}^2 = \sum_{n=1}^{\infty} \pi {\left( \frac{1}{108}\right)}{\left(3^{-(n-1)}\right)}^2$$
=$$\sum_{n=1}^{\infty} \pi {\left( \frac{1}{108}\right)}{\left(3^{-2(n-1)}\right)}$$
=$$\sum_{n=1}^{\infty} \pi {\left( \frac{1}{108}\right)}{\left(\frac{1}{9}\right)}^{n-1}$$
This is a GP with $a = \frac{\pi}{108}$ and $r = \frac{1}{9}$
For infinite terms, the sum of this GP = $\frac{a}{1-r} = \frac{\pi}{96}$
Now, finally,
$$T = \frac{\pi}{12} + 3 \times \frac{\pi}{96} = \frac{11\pi}{96}$$