[Math] Given a line segment $AB$ and a point $P$ inside a circle, can one construct a chord through $P$ congruent to $AB$

euclidean-geometrypuzzle

This is a little exercise found in Robin Hartshorne's Euclid: Geometry and Beyond:
enter image description here

I believe I have found a solution, which only exists when $AB$ has length at least that of the chord bisected by $P$, and length at most the diameter of the circle. So suppose that is the case. I do the following construction. $\odot cXrYZ$ is an abbreviation for the circle centered at $X$ with radius $YZ$. (I assume the compass is not collapsible.) Also, it's not necessary to know my solution to answer my question, so feel free to skip.

  1. Pick $C$ at random on circle $O$. Describe the circle with center $C$ and radius $AB$. Get intersection $D$.
  2. Describe the circle with center $D$ and radius $DC$. This will intersect with the previous circle at $E$ and $F$, say.
  3. Connect $EF$.
  4. Connect $CD$, get intersection $G$.
  5. Draw circle with center $O$ and radius $OG$. (This gives the circle to which all chords of length $AB$ will be tangent to.)
  6. Connect $PO$. Get $H$, the intersection of $PO$ with $\odot cRrOG$. We know this exists, since $P$ must fall outside $\odot cOrOG$.
  7. $\odot cHrPH$. Get $J$.
  8. $\odot cPrPJ$.
  9. $\odot cJrJP$, which will intersect with $\odot cPrPJ$ at $K$ and $L$.
  10. $\odot cOrPO$.
  11. Extend $LK$ through to $M$, the intersection with $\odot cOrPO$.
  12. Connect $MO$, get $N$, the intersection on $\odot cOrOH$.
  13. Extend $PN$ through to intersect the original circle to get $Q$ and $R$. This line is congruent to $AB$ and passes through $P$.

I apologize that this construction may be hard to follow without the picture. This takes me $13$ steps, but I see that Hartshorne suggests it's possible in $5$, hence the (par=$5$). Can anyone produce a more efficient solution in only $5$ steps? I've been thinking about it, but don't see how to make this any simpler from a compass and straightedge construction.

Best Answer

1. Pick an arbitrary point C on the circle. Draw an arc centered at C and radius AB, intersecting the original circle at point D.

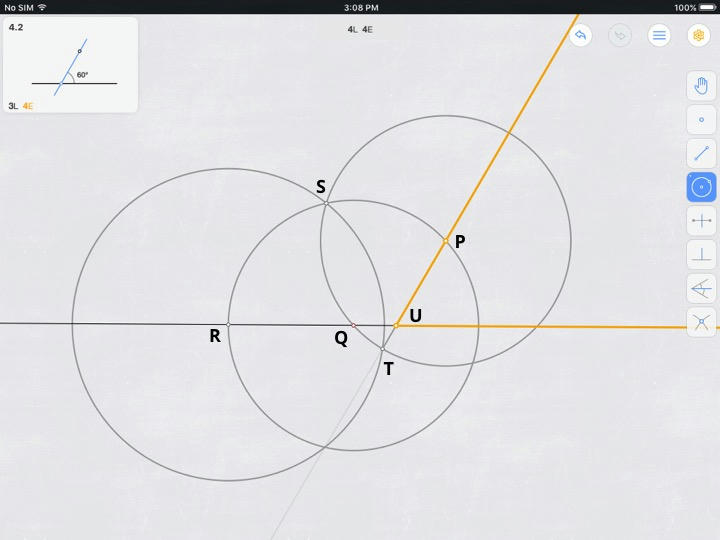
If there is no intersection, stop: AB is too long for a solution to exist.

2. Draw line segment CD.

We now have a chord which is congruent to AB. We need to find a congruent chord which passes through P, so the first thing we need to do is figure out what point on CD will correspond to P.

3. Draw an arc with center O and radius OP. Let this intersect CD in point E.

If there is no intersection, stop: AB is too short for a solution to exist. Otherwise, E is the point we needed. OE is congruent to OP, and CED is congruent to the desired chord. Now if we find the point Q that C corresponds to, we'll have the chord we want.

4. Draw an arc with center P and radius EC to intersect the original circle at point Q.

The (undrawn) triangles OPQ and OEC are congruent, so PQ and EC make the same angle with the radius, and that determines the length of the chord.

5. Draw line segment PQ, extended beyond P to meet the circle on the other side.

This is the desired chord. It is congruent to CD, which is congruent to AB.

Related Question