algebra-precalculustrigonometry
From Stewart Precalculus 5th edi, P407
I am not sure what to do here, in the textbook, Steward didn't provide any example as to finding the terminal point when the distance $t$ is an integer. I know how to find when the distance is in terms of $\pi$.
Am I supposed to replace 1 with $\frac{\pi}{3}$, 2 with $\frac{2\pi}{3}$ and give an estimation?
Since you wanted to see how this is done algebraically, we'll need to look at a particular property of quadratic functions. As I've said in a comment, if $r > 0$, then $ f(x) = rx^2 + sx + t \ $ represents an "upward-opening" parabola. By completing the square, we can write this as
$$f(x) \ = \ r \cdot (x^2 \ + \ \frac{s}{r} \cdot x \ + \ \frac{s^2}{4r^2}) \ + \ (t \ - \ r \cdot \frac{s^2}{4r^2}) \ = \ r \cdot ( \ x + \frac{s}{2r} \ )^2 \ + \ ( \ t - \frac{s^2}{4r} \ ) \ . $$
The vertex of this parabola lies at $ \ x = -\frac{s}{2r} \ $ , with the y-coordinate of the vertex being the minimum value of the function $ \ f(-\frac{s}{2r}) \ = \ t - \frac{s^2}{4r} .$ We will exploit this to reduce the amount of writing we will need to do.
We will label the closest point on the line to $ \ (x_1 , y_1) \ $ as $ \ (X,Y) \ $ . The distance-squared function is
$$D^2 \ = \ ( X - x_1 )^2 \ + \ (Y - y_1)^2 \ = \ ( X - x_1 )^2 \ + \ ( \ [-\frac{AX + C}{B} \ ] - y_1)^2 \ $$
$$= \ ( X - x_1 )^2 \ + \ ( \frac{A}{B} \cdot X \ + \ \frac{C}{B} + \ y_1)^2 \ = \ ( X - x_1 )^2 \ + \ ( \frac{A}{B} \cdot X \ + \ K \ )^2 \ , $$
where we will make a temporary substitution, $ \ K = \frac{C+By_1}{B} \ $ , to further save some writing. (This is often a good idea when working out complicated algebraic expressions, as it reduces the risk of embarrassing, time-wasting errors.) We will see that we can hold out for some time before needing to replace $K$ .
From here, we have
$$D^2 \ = \ ( \ X^2 \ - \ 2x_1X \ + \ x_1^2 \ ) \ + \ ( \ \frac{A^2}{B^2} \cdot X^2 \ + \ 2\frac{A}{B} K \cdot X \ + \ K^2 \ ) \ $$
$$= \ ( \ 1 + \frac{A^2}{B^2} \ ) \cdot X^2 \ + \ 2 ( \ \frac{A}{B} K - x_1 \ ) \cdot X \ + \ ( \ K^2 \ + x_1^2 \ ) , $$
which now has the "general form" for a quadratic function. Since we already know how to convert this to "standard form" by completing the square, we can simply use the results we discussed back at the start. The vertex of the parabola described by this equation lies at
$$X \ = \ -\frac{s}{2r} \ = \ -\frac{2 ( \ \frac{A}{B} K - x_1 \ )}{2( \ 1 + \frac{A^2}{B^2} \ )} \cdot \frac{B^2}{B^2} \ = \ \frac{ B^2 x_1 \ - \ AB K}{A^2 \ + \ B^2 \ } $$
$$= \ \frac{ B^2 x_1 \ - \ AB \cdot (\frac{C+By_1}{B})}{A^2 \ + \ B^2 \ } \ = \ = \ \frac{ B^2 x_1 \ - \ A \cdot (C \ + \ By_1)}{A^2 \ + \ B^2 \ } \ . $$
So here is the x-coordinate of the point on the line that is closest to $(x_1,y_1)$, confirming the stated result without the use of calculus.
We do not bother substituting this into either the quadratic function or the equation for the line, since we know from the standard form of the quadratic function that its minimal value is
$$D^2_{min} \ = \ t - \frac{s^2}{4r} \ = \ ( \ K^2 \ + \ x_1^2 \ ) \ - \ \frac{[ \ 2 ( \ \frac{A}{B} K - x_1 \ ) \ ]^2}{4( \ 1 + \frac{A^2}{B^2} \ )} \cdot \frac{B^2}{B^2} $$
$$= \ ( \ K^2 \ + \ x_1^2 \ ) \ - \ \frac{ ( \ A K \ - \ Bx_1 \ )^2}{ A^2 + B^2} \ = \ \frac{( \ K^2 \ + \ x_1^2 \ )(A^2 + B^2) \ - \ ( \ A K - Bx_1 \ )^2}{ A^2 + B^2} $$
$$= \ \frac{( \ A^2K^2 \ + \ B^2K^2 \ + \ A^2x_1^2 \ + \ B^2x_1^2 \ ) \ - \ ( \ A^2K^2 \ - \ 2ABKx_1 \ + \ B^2x_1^2 \ )}{ A^2 + B^2} $$
$$= \ \frac{ A^2x_1^2 \ + \ 2ABKx_1 \ + \ B^2K^2 \ }{ A^2 + B^2} \ = \ \frac{ ( \ Ax_1 \ + \ BK \ )^2 }{ A^2 + B^2}$$
$$= \ \frac{ ( \ Ax_1 \ + \ B \cdot [\frac{C+By_1}{B}] \ )^2 }{ A^2 + B^2} \ = \frac{ ( \ Ax_1 \ + \ By_1 \ + C \ )^2 }{ A^2 + B^2} \ .$$
Since $ \ \sqrt{x^2} = |x| \ , $ we at last have the relation for the minimum distance,
$$D_{min} \ = \ \frac{ | \ Ax_1 \ + \ By_1 \ + C \ | }{ \sqrt{A^2 + B^2}} \ .$$
It took me a few goes to find a reasonably clean way to develop this by algebra alone. The straight answer to your question about how "an expert" would set this up and proceed is that they wouldn't, but instead would use a more efficient method (such as the ones I linked to in my other answer). That may also explain why one doesn't have much luck finding an approach like this by looking around the internet. In any event, I hope this is what you were inquiring about.
You can use the same intuition when $\theta$ lies in other quadrants, drawing the same line.
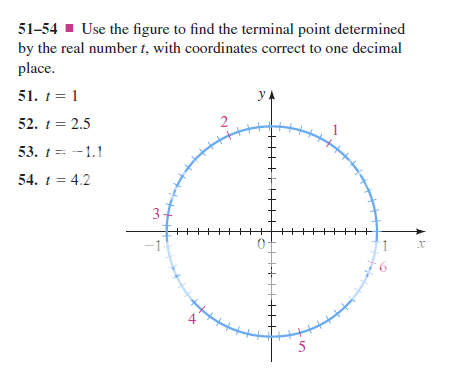
Best Answer
Looking at the figure you can see that he has labels around the edges of the circle. The numbers $1,2,3,4,5,$ and $6$. The terminal point when $t=1$ would correspond to the location labelled with a $1$. The angle at that point is exactly $1$ radian which is about $57$ degrees. By counting the number of tics to get to $1$ you can determine how many radians each tick is worth and then use that to answer questions that involve a fractional number of radians such as $t=2.5$.