We have a point $A(6,0)$ and a line $k:y=2$. Show that the equation of the parabola with a locus $A$ and a directrix $k$ has the formula: $\dfrac{1}{4}x^2-3x+8$.
I had a test on analytic geometry today and this was one of the questions. I was 100% sure that the question was wrong, however, all my classmates told me that they had solved it correctly (apart from the fact that it should have been $-\dfrac{1}{4}$ instead of $\dfrac{1}{4}$, something which I noticed too, disregard this when answering my question). So my question is what I did incorrectly:
We use the formula of a parabola, $y-b=\dfrac{1}{4c}(x-a)^2$. The distance between the directrix and the locus is 2, so $c=1$. We get $y-b=\dfrac{1}{4}(x-a)^2$. We see that the top of the parabola is $T(6,1)$, so we get $y-1=\dfrac{1}{4c}(x-6)^2$. This can also be written as: $y=\dfrac{1}{4}x^2 -12x + 37$. And here we go, a totally different answer. Can anyone point out my mistakes?
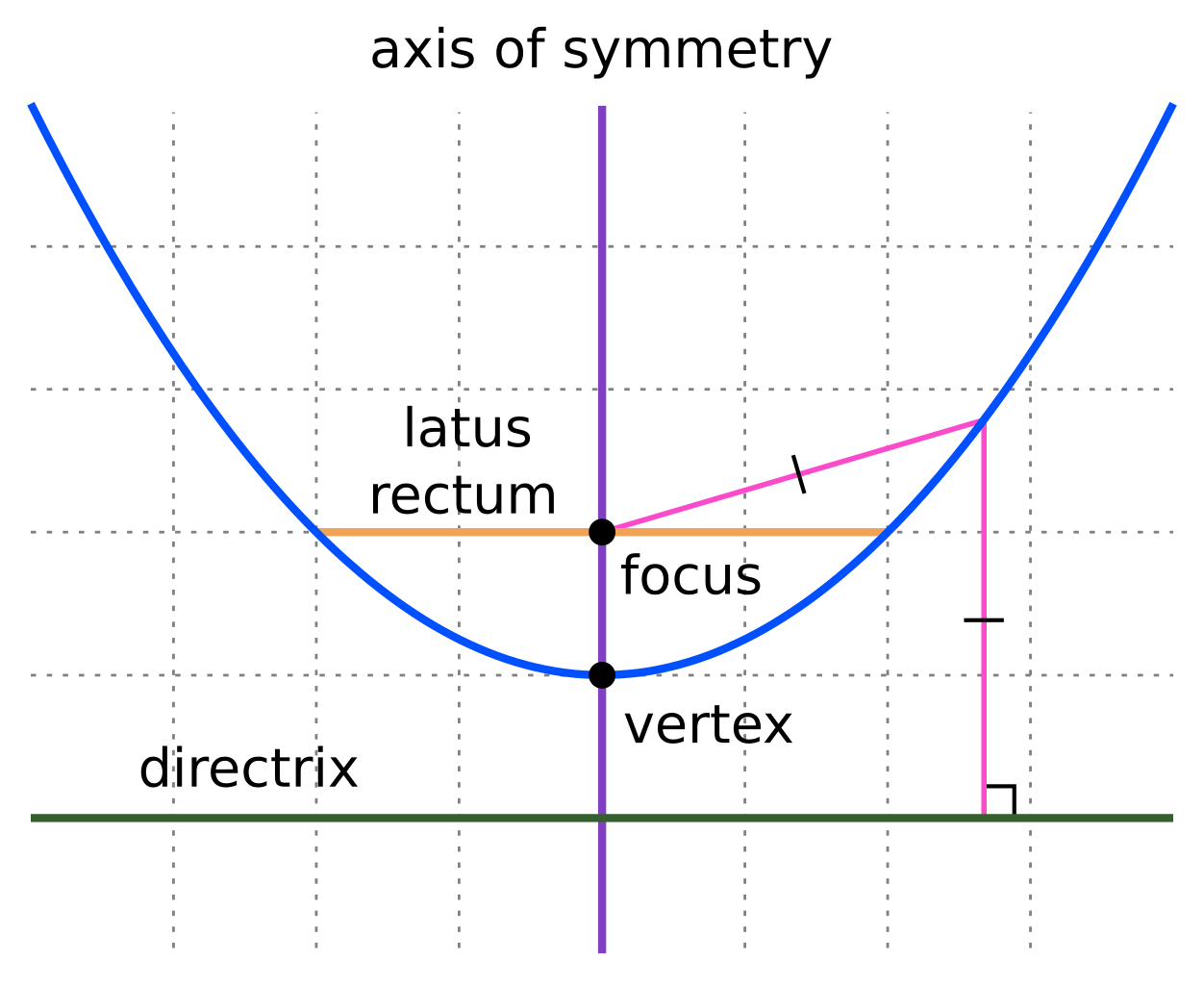it can be seen that the line through the focus and the projection of the given point onto the directrix is perpendicular to the tangent to the given point. Here, these two important points are $(0,6)$ and $(8,0)$ respectively and the line through them has slope $\frac{-6}8=-\frac34$. So the tangent we seek has slope $\frac43$.
Best Answer
If the directrix is the line $y=2$:
Your value of $c$ should be negative, since the focus lies below the directrix. So, your initial equation should be $$\tag{1} y-1={-1\over 4}(x-6)^2.$$ Apart from $c=-1$, and not $c=1$, what you had there is correct.
But, it seems you made some algebraic errors when writing your initial equation in standard form. To write equation $(1)$ in standard form, you could first multiply both sides by $-4$ to obtain $$ -4y+4=(x-6)^2. $$ Now expand the right hand side: $$ -4y+4=x^2-12x+36. $$ So, subtracting $4$ from both sides, we obtain $$-4y=x^2-12 x +32.$$ Finally, divide through by $-4$ $$ y={-1\over4} x^2+3x-8. $$
But then, the proposed solution is incorrect; the right hand side should be multiplied by $-1$. (But the given answer would be correct if the directrix were the line $y=-2$.)