The standard definition of the trig functions is in terms of a unit circle. The classical definition in terms of right triangles is more limited in terms of scope. For this reason in Calculus the more robust definition in terms of the unit circle is used. From this 'standard' definition every identity about the trigonometric functions can be proven.
In your post above you gave the definition in terms of the unit circle, but you left what I think is an important point. When defined in terms of the unit circle the trig functions are 'real valued'. What we mean here is that they are defined in terms of a distance and not some constructed idea called an angle. So let me begin with the definition in terms of the unit circle, then we will move to the sister proof to the one given above for the sine of a difference. From this we can establish the other three identities.
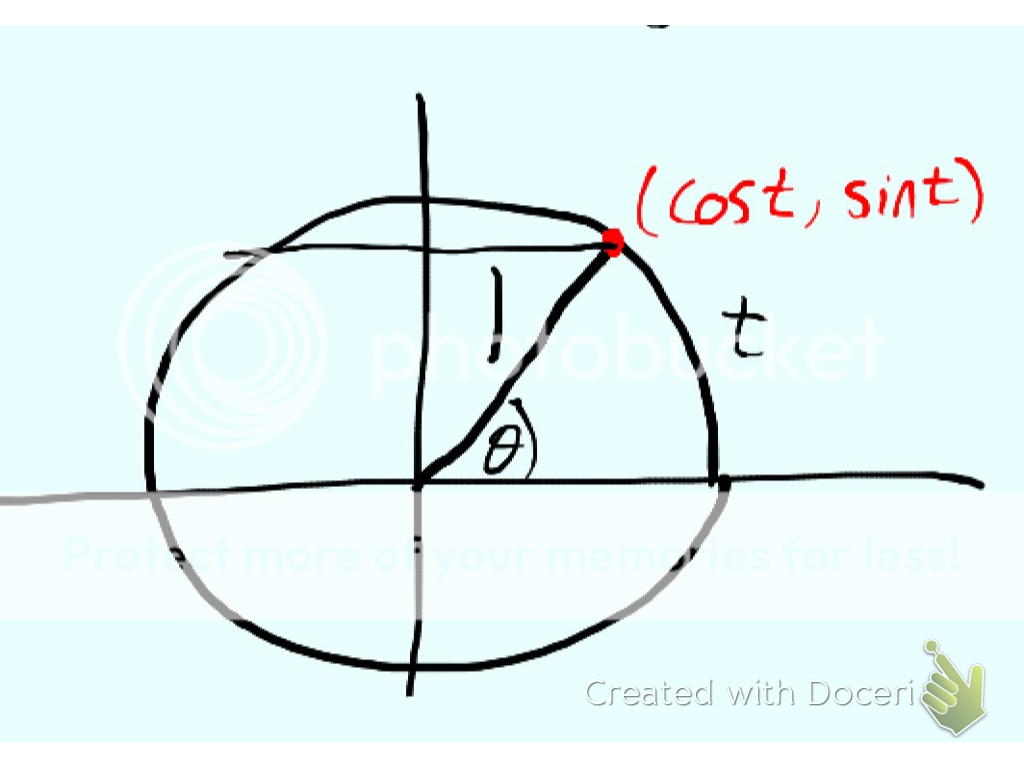
Consider the unit circle
$$ \begin{equation}x^2+y^2 = 1 \end{equation} $$
Starting at the x-intercept (1,0) we travel a distance t around the circle in a counter-clockwise direction (a clockwise movement would be assigned a negative sign). Once we travel a distance t around the circle we end at a point P(x,y) on the circle. We then define
$$ \begin{eqnarray} \cos t = x \\ \sin t = y \end{eqnarray} $$
It then turns out that we can return to angles by noting that on the unit circle the radian measure of the central angle subtended by the arc of length t is equal to t. But we don't need to ever actually return to angles. Our definition stands on its own. Now an immediate consequence of our definition is the familiar Pythagorean identity for sine and cosine.
$$\begin{equation} \cos^2 t + \sin^2 t = 1 \end{equation} $$
(This is obtained by substituting sine and cosine into the unit circle equation for x and y.)
Before we move onto the identity you asked about first let us notice that the sine and cosine functions are periodic. IE.
$$ \cos(a + 2k \pi) = \cos a $$. I believe this is pretty clear because any trip around the circle will take you back to where you started. Make that trip k times and you are still back where you started. For this reason as mentioned above we can assume both angles are in$$ [0, 2 \pi)$$.
Also note that
$$\cos (-t) = \cos t $$ for all real numbers t.
The last thing to address is that rotation is a rigid transformation. In other words when we rotate the plane about a point, the distance between two points before rotation is the same after rotation.
Now we return to the problem. Show that
$$\cos(a-b) = \cos a \cos b + \sin a \sin b $$
Without loss of generality assume $$0<b<a<2 \pi $$
(the case of b=0 is trivial, as is the case of a = 2 $\pi$, and the case a=b, you can verify these yourself)
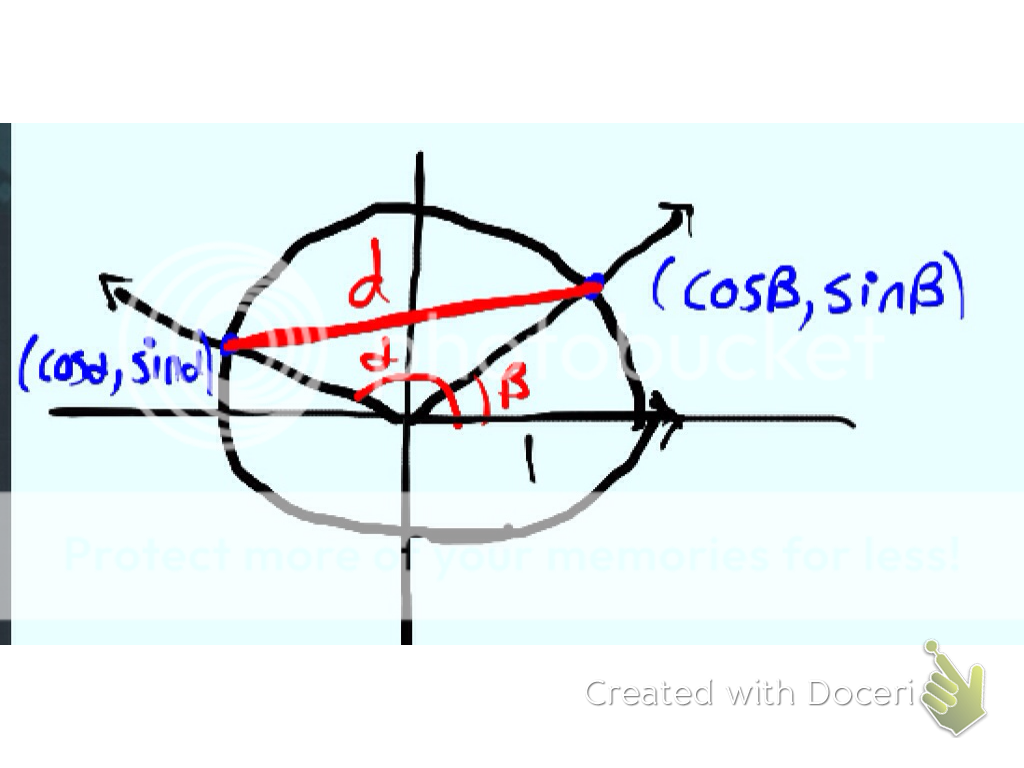
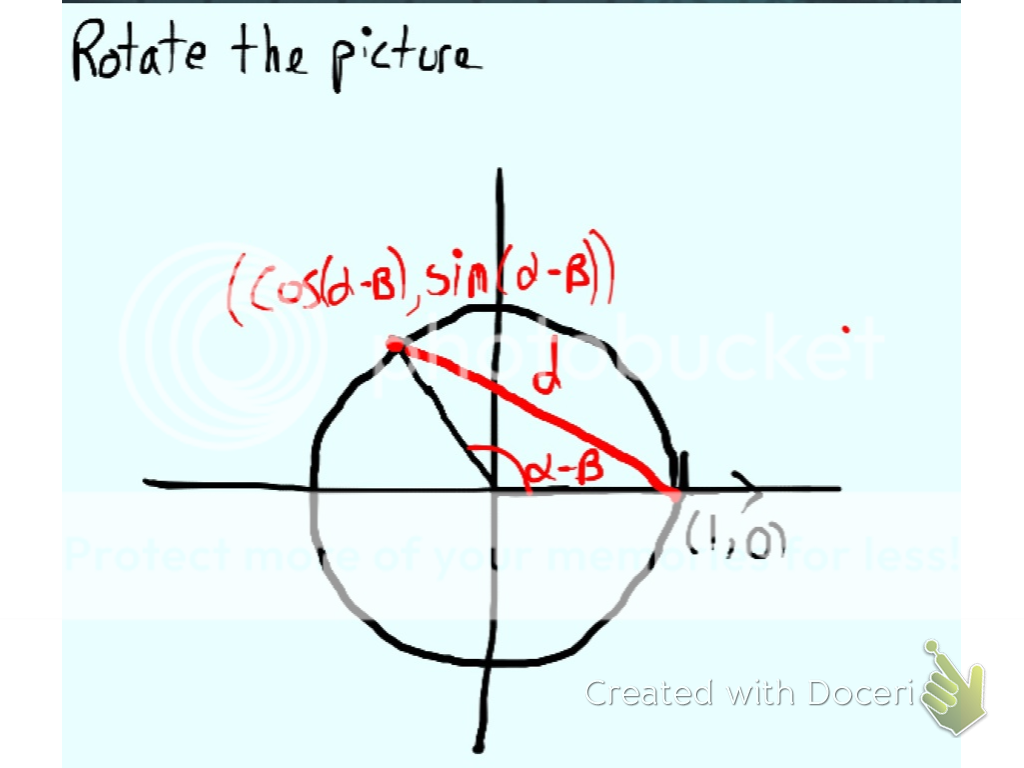
We now consider the points (see diagrams) P($\cos a, \sin b)$ and Q($\cos b, \sin b)$ on the unit circle. We can use the distance formula to find the length of segment PQ. We then rotate the entire plane clockwise through a distance b along the circumference of the circle (or through an angle with radian measure b). This will place point Q at Q`(1,0) and P will now be a distance b-a along the circle from (1,0) so it will be at P`($\cos(a-b), \sin(a-b))$. We now proceed to use the distance formula. Since distance is preserved through rotation segment PQ and segment P`Q` will have the same length.
$$\begin{eqnarray} \sqrt{(\cos a - \cos b)^2 + (\sin a - \sin b)^2} = \sqrt{(\cos(a-b)-1)^2 + (\sin(a-b) - 0)^2} \\ \cos^2 a - 2 \cos a \cos b + \cos^2 b + \sin^2 a - 2 \sin a \sin b + \sin^2 b = \cos^2(a-b) - 2 \cos(a-b) + 1 + \sin^2(a-b) \\ \cos^2 a + \sin^2 a + \cos^2 b + \sin^2 b - 2 \cos a \cos b - 2 \sin a \sin b = \cos^2(a-b) + \sin^2(a-b) + 1 - 2 \cos(a-b) \\ - 2 \cos a \cos b - 2 \sin a \sin b = - 2 \cos(a-b) \\ \cos a \cos b \sin a \sin b = \cos(a-b) \end{eqnarray} $$
Now I assumed $b<a$, is that ok? The answer is yes but you might want to answer why.
Armed with the cosine of the difference formula we can now prove the following.
$$ \begin{eqnarray} \cos(a+b) = \cos(a-(-b)) = \cos a \cos(-b) - \sin a \sin(-b) \\
= \cos a \cos b - \sin a \sin b \end{eqnarray} $$
The last step in the equality comes from our identity for $\cos(-t)$ above and the fact that $\sin(-t) = -\sin(t) $ as was mentioned in the previous post.
Now we can show that $\cos(\frac{\pi}{2} - x) = \sin x$ and in a similar manner to the problem above that $\sin(\frac{\pi}{2} - x) = cos x$. These are your familiar co-function identities. Finally armed with these equations we can now demonstrate the sine of a difference which can then prove the sine of a sum formula.
$$ \begin{eqnarray} \sin(a-b) = \cos(\frac{\pi}{2} - (a-b)) \\ = \cos((\frac{\pi}{2} -a) + b) \\ = \cos(\frac{\pi}{2} -a) \cos b - \sin(\frac{\pi}{2} -a) \sin b \\ = \sin a \cos b - \cos a \sin b \end{eqnarray} $$
And so there we have it. I apologize if the formating is off a bit, still getting used to the system. But now from this identities you can prove most any other basic identity involving the trig functions. All of your double and half angle formulas and your sum-product and product-sum formulas.



Best Answer
I'll amend this eight(!)-year-old answer with more detail.
We begin with the fact that a triangle has three sides. :) In particular, a right triangle has one hypotenuse and two legs. If we take the hypotenuse to have length $1$, and one of the triangle's acute angles to have (radian) measure $\theta$, then the leg opposite $\theta$ has length $\sin\theta$, while the leg adjacent to $\theta$ has length $\cos\theta$. (That's the geometric definition of these values.)
In the diagrams below, $\overline{OP}$ is the hypotenuse of the right triangle in question, and we construct arc $\stackrel{\frown}{PP_0}$ of the unit circle about $O$. Note that, because the radius is $1$, we have $|\stackrel{\frown}{P_0P}| = \theta$.
Following a remarkable construction by Y. S. Chaikovsky (presented in this very readable American Mathematical Monthly article by Leo Gurin), we subdivide the $\stackrel{\frown}{PP_0}$ into $n$ equal parts, recursively building a collection of similar isosceles triangles in various stages. (Each stage has one fewer triangle than its predecessor.) The diagram shows the triangles for $n=4$ and $n=16$, as well as for the limiting case ("$n=\infty$").
For each $n$, the bases of the first stage of triangles form a polygonal approximation of the circular arc $\stackrel{\frown}{P_0P}$; the bases of the second-stage triangles approximation the involute $P_1P$ of that arc; the bases of the third-stage triangles approximate the involute $P_2P$ of that involute; and so on. Moreover, the construction guarantees that the leg of the largest isosceles triangle at each stage has length equal to that of the polygonal path formed by the bases of the previous stage:
$$|\overline{P_{i-1}P_{i}}| = |\widehat{P_{i-1}P}| \tag{1}$$
At the first stage, each triangle has leg-length $1$ and base-length $s := 2\sin\frac{\theta}{2n}$. At the second stage, the smallest triangle has a previous base for a leg, so its base-length is $s^2$; in general, at stage $i$, the smallest triangle's base-length is $s^{i}$. Chaikovsky discovered a clever (but not difficult) combinatorial argument (omitted here) that the total length of all bases at a particular stage is an integer multiple of that smallest base, namely
(a formula that conveniently works for $i=0$ as well, if we rename point $O$ to $P_{-1}$).
Now, as $n$ increases, the various polygonal paths better-approximate their corresponding smooth curves. This is guaranteed by the only sophisticated fact we need from elementary Calculus: $$\lim_{x\to 0} \frac{\sin x}{x} = 1 \qquad\text{so that}\qquad \lim_{n\to \infty}2n\sin\frac{\theta}{2n} = \theta \tag{2}$$ Also, the fraction $(n-j)/n$ better-approximates $1$. Consequently, in the limit, the polygonal paths simplify to curves while the big product in $(\star)$ simplifies to $\theta^i$. Recalling $(1)$, we can write
So what?
Well, observe that, in the limiting diagram, the path $OP_1P_2P_3P_4\cdots$ forms a spiral that appears to (and actually happens to) converge on point $P$. The segments of that path are either perfectly horizontal or perfectly vertical: With each horizontal step, the path alternately over- and under-shoots $P$'s horizontal offset from $O$, while each vertical step does likewise for the vertical offset. But those offsets are precisely $\cos\theta$ and $\sin\theta$! Therefore,
That is, with some simple geometry, a dash of combinatorics, and the slightest touch of Calculus, we arrive at the power series representations for sine and cosine. As my other answer notes, a minor variation in the construction of the involutes (albeit with significantly-trickier combinatorics) leads to the series for tangent and secant. (I still don't have a counterpart for cotangent and cosecant, which remains the topic of my first Trigonography Challenge.) $\square$