[Math] Construct parallel line equidistant from two other parallel lines – Euclidea on iOS challenge 2.8

euclidean-geometrygeometric-constructiongeometry

I bet you know this game, Euclidea – if not I recommend it…
although I'm stuck on level 2.8 which is different on iOS than other platforms for which there are already walk throughs available.

Here is the riddle –
"Construct a straight line parallel to the given parallel lines that lies at equal distance from them"

This is the puzzle prompt

I need to build using compass and ruler an equdistant line between two parallel lines (the equidistant will be parallel to those two). I did it, but there's an additional challenge to do it with 5 moves in this order-
Two circles and 3 lines. Obviously, it's possible to construct a perpendicular to the two parallel lines and then a perpendicular bisector for that one, but 5 steps is pretty tricky.
Is it even possible?! I'm breaking my head over this..

Good luck guys 🙂

Best Answer

EUCLIDEA IOS PROBLEM 2.8 / ANDROID 5.7 | 5E SOLUTION REQUIRED

Given Two parallel lines ${a}$ (for 'above') and ${b}$ ('below'), separated by a distance $2D$.

Goal Construct line ${m}$ (for 'middle') parallel to and equidistant from both given lines, i.e., separated by a distance $D$ from both $a$ and $b$.

Constraints Only an unmarked straightedge and a non-rusty collapsible compass (i.e., a compass that, while on paper, can have any radius but which cannot maintain said radius when not on paper) can be used. Use only from the construction steps below a number of steps that together require just five elementary steps; the fifth step must construct the goal line itself.

  • Construct a point: 0 elementary steps (E).
  • Mark the intersection of two curves with a point: 0E.
  • Construct a new line (*or line segment or ray): 1E.
  • Extend a given line segment (*or ray): 1E.
  • Construct a circle (non-rusty collapsible compass): 1E.
  • Construct the perpendicular bisector of a line segment: 3E.
  • Construct a new line perpendicular to an old line: 3E.

Hints from Euclidea (including Twitter support) A known 5E solution employs five elementary steps in the order: circle, circle, line, line, line. The first circle is twice the radius of the second one. Homothety is used in the known solution.

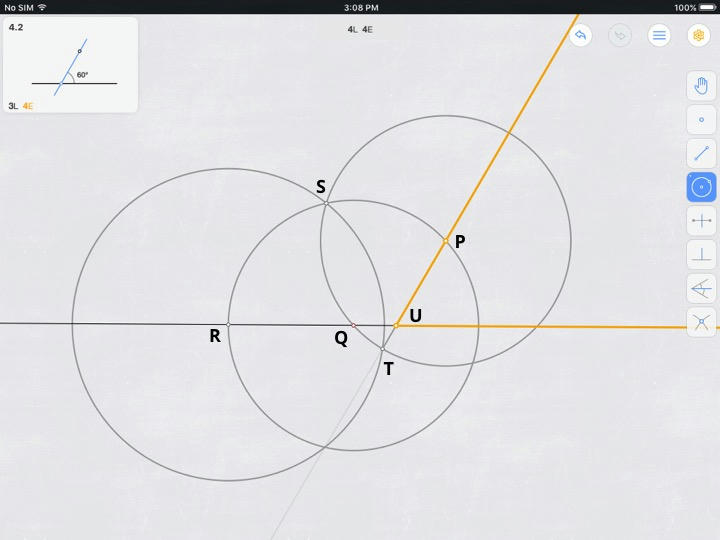
SOLUTION Please refer to the figure below. Apologies for not having labels on this figure.

  1. Construct two arbitrary points $O$ and $P$ on $b$ separated by a distance $OP > D$ (just eyeball it) [OE running total].

  2. Construct circle $P(O)$ centered on point $P$ and with radius $OP$ [1E running total].

    • $P(O)$ intersects $b$ at a new point $Q$.

  3. Construct $Q(O)$ [2E running total].

    • $Q(O)$ also intersects $a$ at two points $L$ (for 'left') and $R$ ('right').

  4. Construct $\overleftrightarrow{OL}$ [3E running total].

    • $P(O)$ intersects $\overleftrightarrow{OL}$ at $O$ and another point $M_L$.

  5. Construct $\overleftrightarrow{OR}$ [4E running total].

    • $P(O)$ intersects $\overleftrightarrow{OR}$ at $O$ and another point $M_R$.

  6. Construct the desired line $m = \overleftrightarrow{M_{L}M_{R}}$, shown in yellow in the figure below [5E final total].

5S solution to this problem

PROOF OF THE SOLUTION

  1. Given that $OP$ is chosen such that $OQ$ is larger than the gap $2D$ between the two give lines, there exist exactly two points $L$ and $R$ of intersection between $Q(O)$ and $a$.

  2. Homothety is then used in this construction. First, we define a homothetic point ${O}$ on one of the lines, with $b$ used here without loss of generality. $Q(O)$ is constructed to have twice the radius of $P(O)$. Hence, taking $O$ as the homothetic point, also known as the center of dilation, we can view $P(O)$ as the half-fold 'dilation' of $Q(O)$. This means that every line through $O$ intersects $P(O)$ and $Q(O)$ at corresponding points, with the point on $P(O)$ half as far from $O$ as its corresponding point on $Q(O)$ is.

  3. More specifically, the point $M_L$ on $P(O)$ that corresponds to the point $L$ on $P(O)$ can be found by intersecting $\overleftrightarrow{OL}$ and $P(O)$. Point $M_R$ can also be found analogously using $R$.

  4. Homothety preserves parallelism. Therefore, line $m := \overleftrightarrow{M_LM_R}$ is parallel to both $a$ and $b$, as desired.

  5. Given that the homothety involved here involves a half-fold dilation of $Q(O)$ to $P(O)$, we know that the gap between $a$ and $m$ is also half of the gap between $a$ and $b$. This is equivalent to saying that $m$ is equidistant from both $a$ and $b$, as desired. $\blacksquare$

Related Question