Assume the following process:
- Let's start with the set of primes $\{p_k\}$
- Then we use the Euler product being equivalent to Riemann's Zeta function
$$
\prod_{p \text{ prime}} \frac{1}{1-p^{-s}} = \sum_{n=1}^\infty\frac{1}{n^s} = \zeta(s).
$$ - Now $\rho$, the non-trivial roots of $\zeta(s)$, contribute to the Prime Counting Function $\pi(x)$ in the following way
$$\pi(x) = \operatorname{R}(x) – \sum_{\rho}\operatorname{R}(x^{\rho}) – \frac1{\ln x} + \frac1\pi \arctan \frac\pi{\ln x} ,
$$
with $ \operatorname{R}(x) = \sum_{n=1}^{\infty} \frac{ \mu (n)}{n} \operatorname{li}(x^{1/n})$.
(Very nice demonstration can be found here.) - The $k$th prime $p_k$ can now be calutated by using $\pi(p_k)=k$.
- So we get back to where we started: (1.) the set of primes $\{p_k\}$ and we now could start again.
My question is: What if a certain prime is missing at the beginning? Will the missing prime be generated automatically, if you iterate the process above?
It would also be interesting to see how the roots are distributed. Are they still lying on the critical line $1/2+iz$?
Is there an easy way to calculate the roots directly from the Euler Product?
Sorry for not going into details, but I think it's all common online knowledge from here and there.
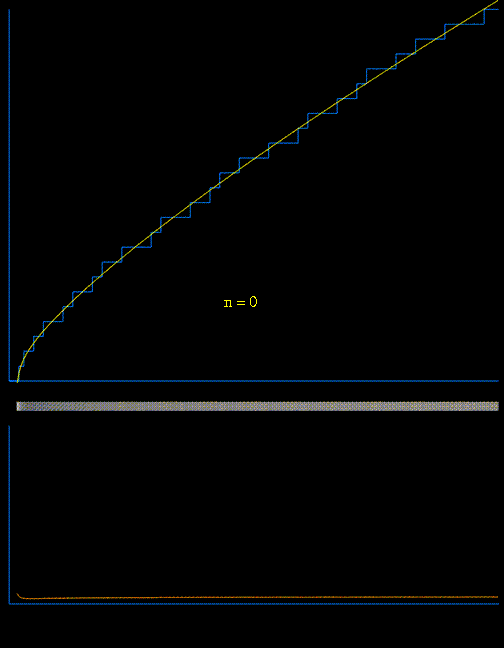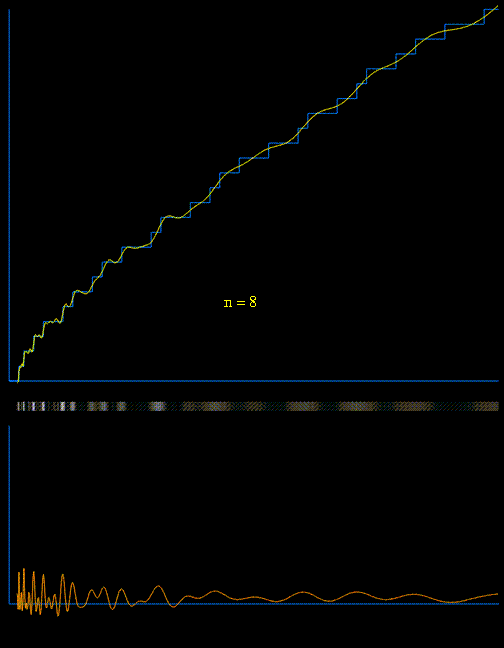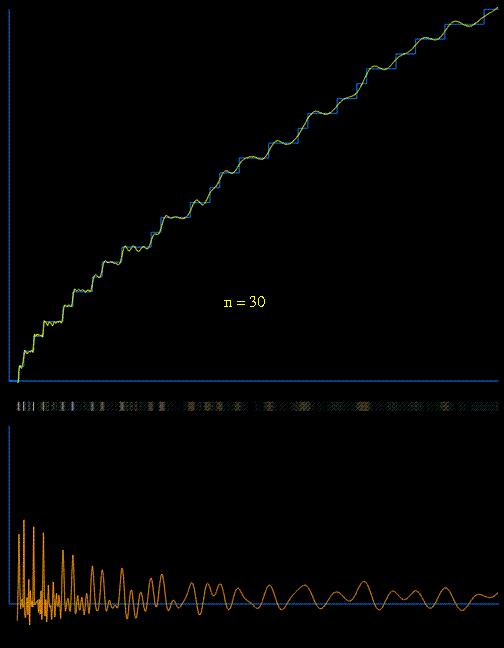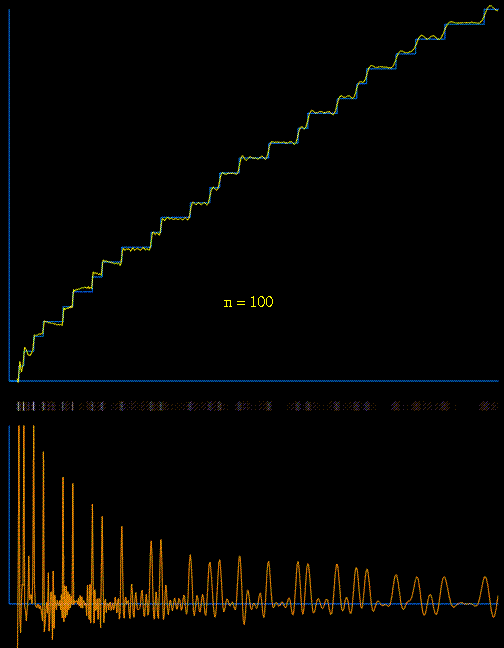
Best Answer
Leaving some primes out of the Euler product won't affect the location of the zeroes, since you will end up with the Zeta function multiplied by a non-zero analytic function (which won't produce any more zeros), and the formula for the prime counting function depends only on the location of the zeroes. So as far as I understand your algorithm, yes, it will "regenerate" any (finite number of) primes that were initially missing.
EDIT: Corrected my erroneous description of the missing term as "constant".
EDIT: To show that the analytic continuation of the product is the same as the product of the analytic continuation, use the fact that the analytic continuation is unique: "Let $f_1$ and $f_2$ be analytic functions on domains $\Omega_1$ and $\Omega_2$, respectively, and suppose that the intersection $\Omega_1 \cap \Omega_2$ is not empty and that $f_1 = f_2$ on $\Omega_1 \cap \Omega_2$. Then $f_2$ is called an analytic continuation of $f_1$ to $\Omega_2$, and vice versa (Flanigan 1983, p. 234). Moreover, if it exists, the analytic continuation of $f_1$ to $\Omega_1$ is unique." We will also need the fact that $\zeta(s)$ and $1-p^{-s}$ are analytic (and the more basic fact that the product of two analytic functions is analytic).
COMMENT: I think your idea here is pretty interesting! I suspect that it may work even in some cases where an infinite number of primes are discarded.