It should be the case that, in some appropriate sense
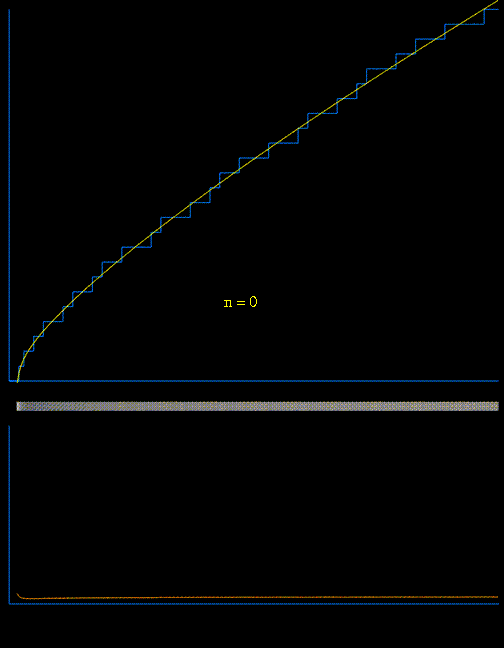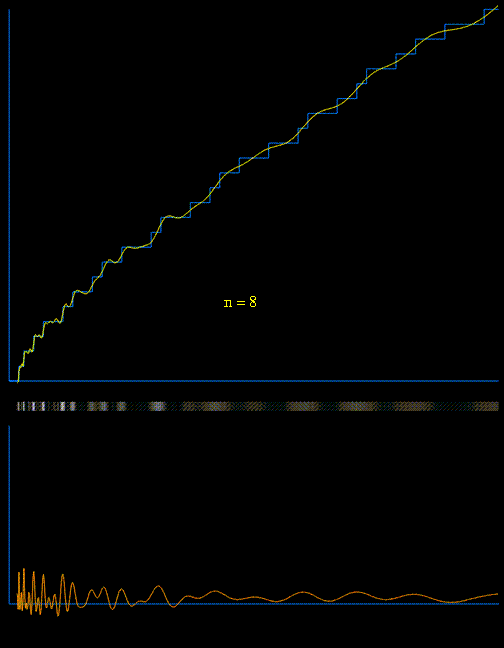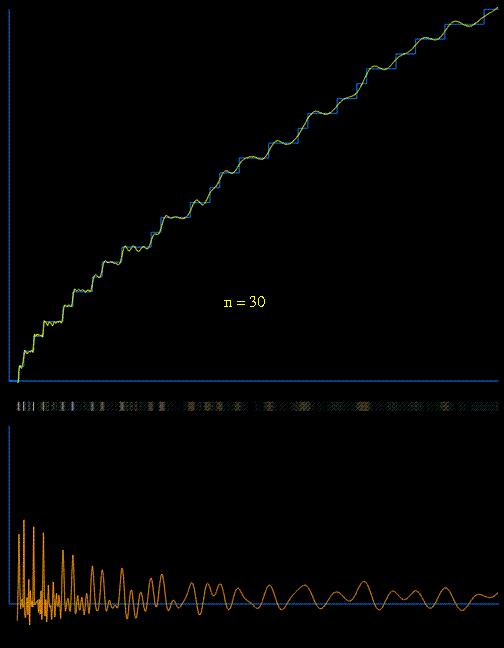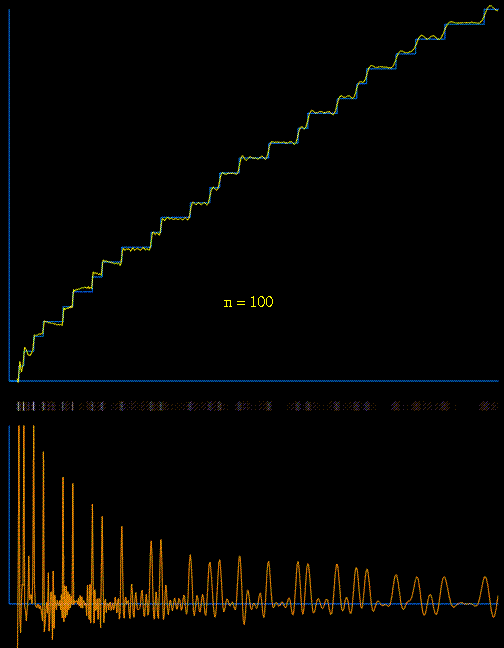
$$\pi (x)\sim \operatorname{Ri}(x)-\sum_{\rho}\operatorname{Ri}(x^{\rho}) \tag*{(4)}$$
with $\operatorname{Ri}$ denoting the Riemann function defined:
$$\operatorname{Ri}(x)=\sum_{m=1}^\infty \frac{\mu (m)}{m}\operatorname{li}\left(x^{\frac{1}{m}}\right). \tag*{(5)}$$
This relation $(4)$ has been called "exact" [in Ribenboim's The New Book of Prime Number Records], yet we could not locate a proof in the literature; such a proof should be nontrivial, as the conditionally convergent series involved are problematic. In any case relation $(4)$ is quite accurate, and furthermore the Riemann function $\operatorname{Ri}$ can be calculated efficiently (…) The sum in $(4)$ over critical zeros is not absolutely convergent, and furthermore the phases of the summands interact in a frightfully complicated way.
—from Journal of Computational and Applied Mathematics by Borwein et al.
Of profound importance, Bernhard Riemann proved that the prime-counting function is exactly
$$\pi (x)=\operatorname{R}(x)-\sum_{\rho}\operatorname{R}(x^{\rho})$$
where
$$\operatorname{R}(x)=\sum_{n=1}^\infty \frac{\mu (n)}{n}\operatorname{li}\left(x^{\frac{1}{n}}\right),$$
(…) $\rho$ indexes every zero of the Riemann zeta function, and $\operatorname{li}\left(x^{\frac{1}{n}}\right)$ is not evaluated with a branch cut but instead considered as $\operatorname{Ei}\left(\frac{\rho}{n}\ln x\right)$. Equivalently, if the trivial zeros are collected and the sum is taken only over the non-trivial zeros $\rho$ of the Riemann zeta function, then $\pi (x)$ may be written
$$\pi (x)=\operatorname{R}(x)-\sum_{\rho}\operatorname{R}(x^{\rho})-\frac{1}{\ln x}+\frac{1}{\pi}\arctan\frac{\pi}{\ln x}.$$
—from Wikipedia's Prime counting function article
Questions:
-
According to Borwein and Ribenboim, the index in $(4)$ should run only over non-trivial zeros. According to Wikipedia, the index in $(4)$ should run over all zeros. Wikipedia states that if the sum runs only over non-trivial zeros, then we add the $\ln$ and $\arctan$ terms, which is even more confusing. So what's true?
-
I'm pretty sure that Riemann did not prove the formula $(4)$. He only proposed a "weaker" form of it, namely
$$\pi (x)=\sum_{m=1}^\infty \frac{\mu (m)}{m}J\left(x^{\frac{1}{m}}\right)$$
where
$$J(x)=\operatorname{li}(x)-\sum_{\rho}\operatorname{li}\left(x^{\rho}\right)+\int_x^\infty \frac{dt}{t(t^2-1)\ln t}-\ln 2$$
and where $\rho$ runs over all non-trivial zeros. The formula was proven by Mangoldt, not Riemann. The Wikipedia article is wrong in that historical fact, isn't it? -
Even though the proof of $(4)$ is nowhere to be found in the literature, Raymond Manzoni provided a partial proof here: Two Representations of the Prime Counting Function.
I call it partial because it is unknown whether the series converges at all: How could that be settled down?
Note: When I refer to the formula $(4)$ in this question, I assume $=$ instead of $\sim$.
Best Answer
Now posted on MathOverflow by vitamin d: https://mathoverflow.net/questions/386213/is-pi-x-operatornamerx-sum-rho-operatornamerx-rho-correct-a/398456#398456