I have a point $Q$ in 3D space whose coordinates are defined by two parameters, $u$ and $v$. The definitions of its coordinates are extremely long, based upon the positions of three fixed points and two variable points. I've been trying to simplify them, but with little success.
I've tried working forward, starting at the beginning of the derivation with the full algebraic expressions and attempting to simplify the expressions at each step towards building the final definitions, and working backward, starting at the final definitions with symbolic placeholders and attempting to group and cancel the placeholders; neither process has yielded much reduction in the complexity of the coordinate definitions.
I had more success with other points in this project defined in a similar manner. I'm not sure why this one in particular is giving me so much trouble.
The coordinate definitions for $Q(u, v)$ are derived with the following procedure.
- Define three fixed points which are all located on the surface of a sphere with radius $a$ centered on the origin:
- $P_S = (X_S, Y_S, Z_S) = \left(\frac{2 + \sqrt{2}}{4} a, \left(\frac{\sqrt{3}}{6} – \frac{\sqrt{6}}{4}\right) a, -\frac{\sqrt{6}}{6} a\right)$
- $P_T = (X_T, Y_T, Z_T) = \left(0, \frac{2 \sqrt{3} – \sqrt{6}}{6} a, \frac{2 \sqrt{3} + \sqrt{6}}{6} a\right)$
- $P_P = (-X_S, Y_S, Z_S) = \left(-\frac{2 + \sqrt{2}}{4} a, \left(\frac{\sqrt{3}}{6} – \frac{\sqrt{6}}{4}\right) a, -\frac{\sqrt{6}}{6} a\right)$
- Define three single-variable functions:
- $X(t) = \frac{a}{\sqrt{2}} \frac{\cos\left(\frac{π}{2} t\right) + \sin\left(\frac{π}{2} t\right)}{(\sqrt{2} – 2) \left(\cos\left(\frac{π}{2} t\right) + 1\right) – 1}$
- $Y(t) = -\frac{a}{\sqrt{6}} \frac{(4 \sqrt{2} – 3) \cos\left(\frac{π}{2} t\right) + \sin\left(\frac{π}{2} t\right) + 4 \sqrt{2} – 4}{(\sqrt{2} – 2) \left(\cos\left(\frac{π}{2} t\right) + 1\right) – 1}$
- $Z(t) = \frac{a}{\sqrt{3}} \frac{\sqrt{2} \cos\left(\frac{π}{2} t\right) – 2 \sin\left(\frac{π}{2} t\right) + \sqrt{2} – 1}{(\sqrt{2} – 2) \left(\cos\left(\frac{π}{2} t\right) + 1\right) – 1}$
- Define two variable points which vary with $u$ and $v$, respectively, and which also lie on the surface of the same sphere as the three fixed points:
- $P_u = (X(u), Y(u), Z(u))$
- $P_v = (-X(v), Y(v), Z(v))$
- Find the normal vector $\vec{n_u}(u)$ of the plane which passes through $P_u$, $P_T$, and $P_P$ and the normal vector $\vec{n_v}(v)$ of the plane which passes through $P_v$, $P_T$, and $P_S$ by subtracting the first point in each trio from the second and third points in each trio and taking the cross products of the resulting pairs of vectors:
$$
\vec{n_u}(u) = \begin{pmatrix}
\bigl( Y_S – Y(u)\bigr) ⋅ \bigl(Z_T – Z(u)\bigr) – \bigl( Z_S – Z(u)\bigr) ⋅ \bigl(Y_T – Y(u)\bigr),\\
\bigl( Z_S – Z(u)\bigr) ⋅ \bigl(X_T + X(u)\bigr) – \bigl(-X_S + X(u)\bigr) ⋅ \bigl(Z_T – Z(u)\bigr),\\
\bigl(-X_S + X(u)\bigr) ⋅ \bigl(Y_T – Y(u)\bigr) – \bigl( Y_S – Y(u)\bigr) ⋅ \bigl(X_T + X(u)\bigr)
\end{pmatrix}
$$
$$
\vec{n_v}(v) = \begin{pmatrix}
\bigl(Y_S – Y(v)\bigr) ⋅ \bigl(Z_T – Z(v)\bigr) – \bigl(Z_S – Z(v)\bigr) ⋅ \bigl(Y_T – Y(v)\bigr),\\
\bigl(Z_S – Z(v)\bigr) ⋅ \bigl(X_T – X(v)\bigr) – \bigl(X_S – X(v)\bigr) ⋅ \bigl(Z_T – Z(v)\bigr),\\
\bigl(X_S – X(v)\bigr) ⋅ \bigl(Y_T – Y(v)\bigr) – \bigl(Y_S – Y(v)\bigr) ⋅ \bigl(X_T – X(v)\bigr)
\end{pmatrix}
$$ - Find the direction vector of the line formed by the intersection of the two planes by taking the cross product of the two normal vectors:
$$
\vec{d}(u, v) = \bigl(X_d(u, v), Y_d(u, v), Z_d(u, v)\bigr) = \begin{pmatrix}
\Bigl(\bigl( Z_S – Z(u)\bigr) ⋅ \bigl(X_T + X(u)\bigr) – \bigl(-X_S + X(u)\bigr) ⋅ \bigl(Z_T – Z(u)\bigr)\Bigr)\\
⋅\Bigl(\bigl(X_S – X(v)\bigr) ⋅ \bigl(Y_T – Y(v)\bigr) – \bigl(Y_S – Y(v)\bigr) ⋅ \bigl(X_T – X(v)\bigr)\Bigr)\\
-\Bigl(\bigl(-X_S + X(u)\bigr) ⋅ \bigl(Y_T – Y(u)\bigr) – \bigl( Y_S – Y(u)\bigr) ⋅ \bigl(X_T + X(u)\bigr)\Bigr)\\
⋅\Bigl(\bigl(Z_S – Z(v)\bigr) ⋅ \bigl(X_T – X(v)\bigr) – \bigl(X_S – X(v)\bigr) ⋅ \bigl(Z_T – Z(v)\bigr)\Bigr),\\
\Bigl(\bigl(-X_S + X(u)\bigr) ⋅ \bigl(Y_T – Y(u)\bigr) – \bigl( Y_S – Y(u)\bigr) ⋅ \bigl(X_T + X(u)\bigr)\Bigr)\\
⋅\Bigl(\bigl(Y_S – Y(v)\bigr) ⋅ \bigl(Z_T – Z(v)\bigr) – \bigl(Z_S – Z(v)\bigr) ⋅ \bigl(Y_T – Y(v)\bigr)\Bigr)\\
-\Bigl(\bigl( Y_S – Y(u)\bigr) ⋅ \bigl(Z_T – Z(u)\bigr) – \bigl( Z_S – Z(u)\bigr) ⋅ \bigl(Y_T – Y(u)\bigr)\Bigr)\\
⋅\Bigl(\bigl(X_S – X(v)\bigr) ⋅ \bigl(Y_T – Y(v)\bigr) – \bigl(Y_S – Y(v)\bigr) ⋅ \bigl(X_T – X(v)\bigr)\Bigr),\\
\Bigl(\bigl( Y_S – Y(u)\bigr) ⋅ \bigl(Z_T – Z(u)\bigr) – \bigl( Z_S – Z(u)\bigr) ⋅ \bigl(Y_T – Y(u)\bigr)\Bigr)\\
⋅\Bigl(\bigl(Z_S – Z(v)\bigr) ⋅ \bigl(X_T – X(v)\bigr) – \bigl(X_S – X(v)\bigr) ⋅ \bigl(Z_T – Z(v)\bigr)\Bigr)\\
-\Bigl(\bigl( Z_S – Z(u)\bigr) ⋅ \bigl(X_T + X(u)\bigr) – \bigl(-X_S + X(u)\bigr) ⋅ \bigl(Z_T – Z(u)\bigr)\Bigr)\\
⋅\Bigl(\bigl(Y_S – Y(v)\bigr) ⋅ \bigl(Z_T – Z(v)\bigr) – \bigl(Z_S – Z(v)\bigr) ⋅ \bigl(Y_T – Y(v)\bigr)\Bigr)
\end{pmatrix}
$$ - Find the scalar $r(u, v)$ to multiply with $\vec{d}(u, v)$ so that translating point $P_T$ by the scaled vector places the new point on the surface of the same sphere whose surface all other points are located upon:
- $r(u, v) = a ⋅ \frac{\left(\sqrt{2} – 2\right) ⋅ Y_d(u, v) – \left(2 + \sqrt{2}\right) ⋅ Z_d(u, v)}{\sqrt{3} ⋅ (X_d(u, v)^2 + Y_d(u, v)^2 + Z_d(u, v)^2)}$
- Finally, translate the point $P_T$ by $r(u, v) ⋅ \vec{d}(u, v)$ to obtain the point whose position we are calculating:
- $Q(u, v) = (X_Q(u, v), Y_Q(u, v), Z_Q(u, v)) = (X_T + r(u, v) ⋅ X_d(u, v), Y_T + r(u, v) ⋅ X_d(u, v), Z_T + r(u, v) ⋅ Z_d(u, v))$
Context
I am working on parametrically defining a 3D surface of constant width, specifically a symmetric spheroform tetrahedron with corner radius $a$. The object is constructed as follows:
- Start with a regular tetrahedron with edge-length $1$.
- Each flat face is replaced with with a triangular section of a sphere of radius $1 + a$ centered on the vertex which is opposite that face.
- Each edge consists of a section of a channel surface defined as the envelope of a sphere of radius $\frac{(4 \sqrt{2} – 8) t^2 + 2 – \sqrt{2}}{8} + a$ positioned such that it is tangent to the two faces that meet at that edge and to the corresponding edge of the base tetrahedron, moving from one vertex of the edge at $t = -\frac{1}{2}$ to the center of the edge at $t = 0$ to the other vertex of the edge at $t = \frac{1}{2}$.
- Finally, at each vertex of the tetrahedron place a section of a sphere with radius $a$ to join the boundaries of the three channel surfaces which meet at that vertex.
My goal is to parameterize each of the three types of surface patch (face, edge, and vertex) in two parameters, $u$ and $v$, such that
- dividing the surfaces with equal steps in $u$ and $v$ gives a reasonably-uniform distribution of points on each patch;
- assuming the same step size, the points on the boundary of any one patch align perfectly with the points on the boundaries of its neighboring patches; and
- no more than six helper-variables/sub-functions are used in total in the definitions of all three coordinates of each patch-defining-point, and all the functions/variables are continuous over the restricted input domain, due to limitations of the 3D software I am using (Blender).
Because the object is fully symmetrical, I only need to work out one of each face, edge, and vertex, and the remainder can be obtained through rotations and reflections.
So far, I (with help from Stack Exchange users) have successfully parameterized and greatly simplified the face patch and edge patch of the spheroform tetrahedron as 3D surfaces defined by points in two parameters. The vertex patch, parameterized but not at all simplified, is the subject of this question.
Face
$$
Q_F(u, v) = \begin{pmatrix}\begin{aligned}
(1 + a) × &\left(\frac{\sqrt{1}}{2} × f(u, v) × \left(\frac{h(u)}{g(u)} – \frac{h(u)}{g(u)}\right)\right),\\
(1 + a) × &\left(\frac{\sqrt{3}}{2} × f(u, v) × \left(\frac{h(u)}{g(u)} + \frac{h(u)}{g(u)}\right) – \frac{2 \sqrt{3} + \sqrt{6}}{6}\right),\\
-(1 + a) × &\left(\frac{\sqrt{3}}{2} × f(u, v) × \left(\frac{h(u)}{g(u)} × \frac{h(u)}{g(u)}\right) – \frac{2 \sqrt{3} – \sqrt{6}}{6} – 1\right)
\end{aligned}\end{pmatrix}
$$
where
$$
f(u, v) = 2 × g(u) × g(v) × \frac{(2 + \sqrt{2}) × (g(v) × h(u) + g(u) × h(v)) + (2 – \sqrt{2}) × h(u) × h(v)}{3 × h(u)^2 × \bigl(g(v)^2 + h(v)^2\bigr) + \bigl(g(v) × h(u) + 2 × g(u) × h(v)\bigr)^2}
$$
$$
\begin{aligned}
g(t) = \frac{2 \sqrt{3} + 1 \sqrt{6}}{12} – \frac{1 \sqrt{3} + \sqrt{6}}{3} × &\frac{1}{2 \cos\left(\frac{π}{2} t\right) + \sqrt{2} + 4} × \left(3 \sin\left(\frac{π}{2} t\right) + \cos\left(\frac{π}{2} t\right)\right)
\\
h(t) = \frac{4 \sqrt{3} + 3 \sqrt{6}}{ 6} – \frac{8 \sqrt{3} + 6 \sqrt{6}}{3} × &\frac{1}{2 \cos\left(\frac{π}{2} t\right) + \sqrt{2} + 4}
\end{aligned}
$$
Edge
$$
Q_E(u, v) = \begin{pmatrix}
\frac{1 + \sqrt{2}}{2} \tan\left(\frac{π}{4} u\right) \left(1 – j(u, v)\right), \\
\frac{1 \sqrt{3} + \sqrt{6}}{12} \left(\tan\left(\frac{π}{4} u\right)^2 – 1 – \left(\tan\left(\frac{π}{4} u\right)^2 + \left(\tan\left(\frac{π}{4} v\right) + 1\right)^2 – 3\right) j(u, v)\right), \\
\frac{2 \sqrt{3} + \sqrt{6}}{24} \left(\tan\left(\frac{π}{4} u\right)^2 + 5 – 6 \sqrt{2} – \left(\tan\left(\frac{π}{4} u\right)^2 + \left(\tan\left(\frac{π}{4} v\right) – 2\right)^2 – 6\right) j(u, v)\right) + 1 + a
\end{pmatrix}
$$
where
$$
j(u, v) = \frac{\sec\left(\frac{π}{4} u\right)^2 + 2 (\sqrt{2} – 2) (1 + 2 a)}{\sec\left(\frac{π}{4} u\right)^2 + \sec\left(\frac{π}{4} v\right)^2}
$$
Vertex
Translated so the sphere of radius $a$ is located at the origin, we get the topic of this question, so $Q_V(u, v) = Q(u, v) + \left(0, \frac{\sqrt{3}}{3}, -\frac{\sqrt{6}}{3} + 1 + a\right)$.
Visualized in GeoGebra
This GIF shows the outline of each surface patch in dark green curves, with red curves crossing the centers of each patch. All red and green curves are composed of circular arcs. The base tetrahedron is shown in brown. One vertex-sphere is shown in orange, with bright green circular arcs denoting the boundary of that vertex's surface patch and extended to full circles on the surface of the sphere with dark blue arcs. A cyan line passes through that vertex, the center of the vertex-sphere-patch, the centroid of the base tetrahedron, and the center of the face opposite the highlighted vertex.
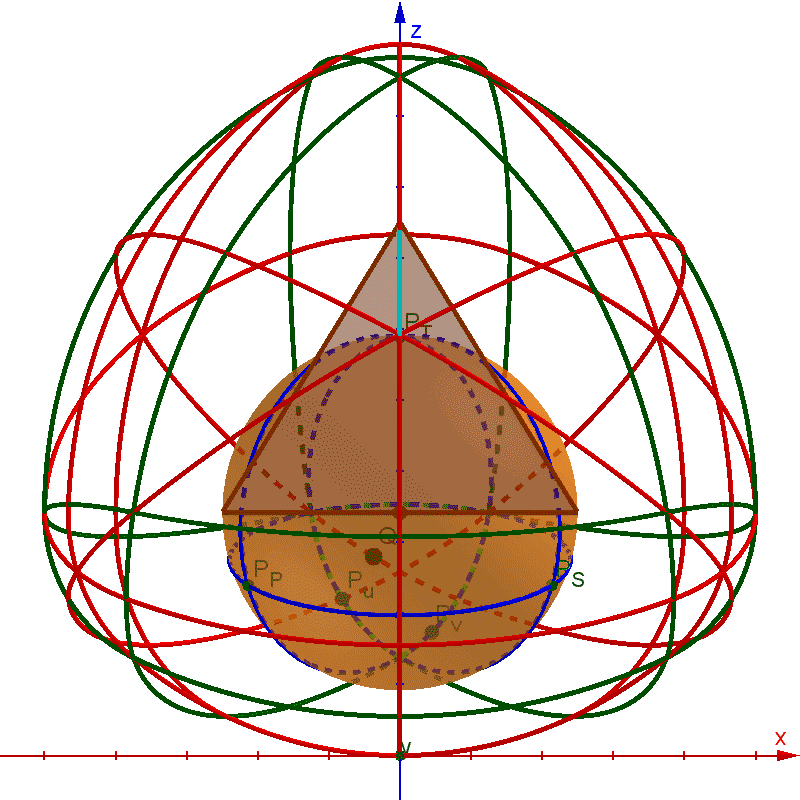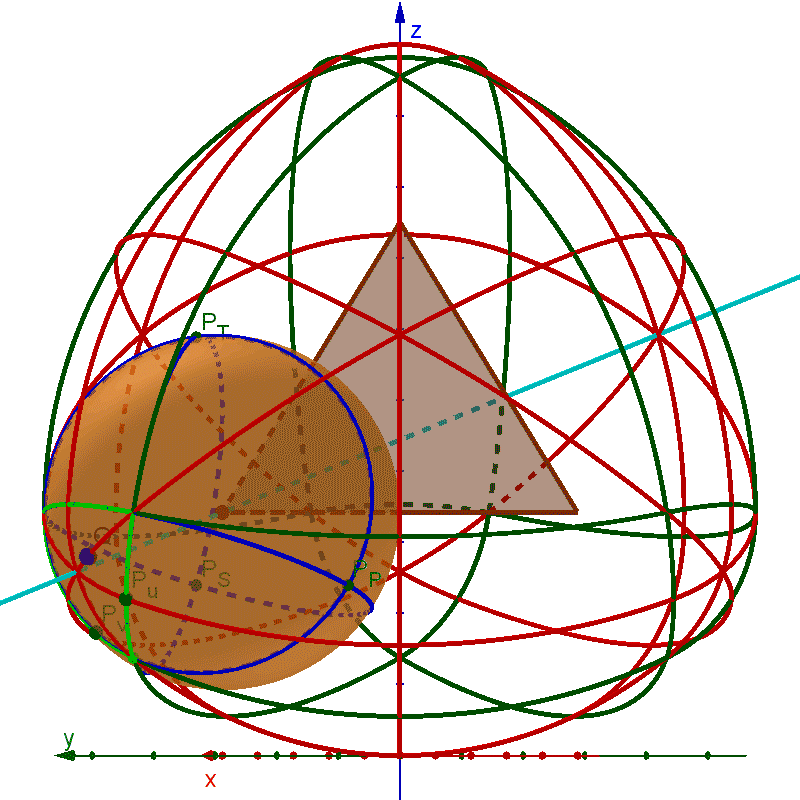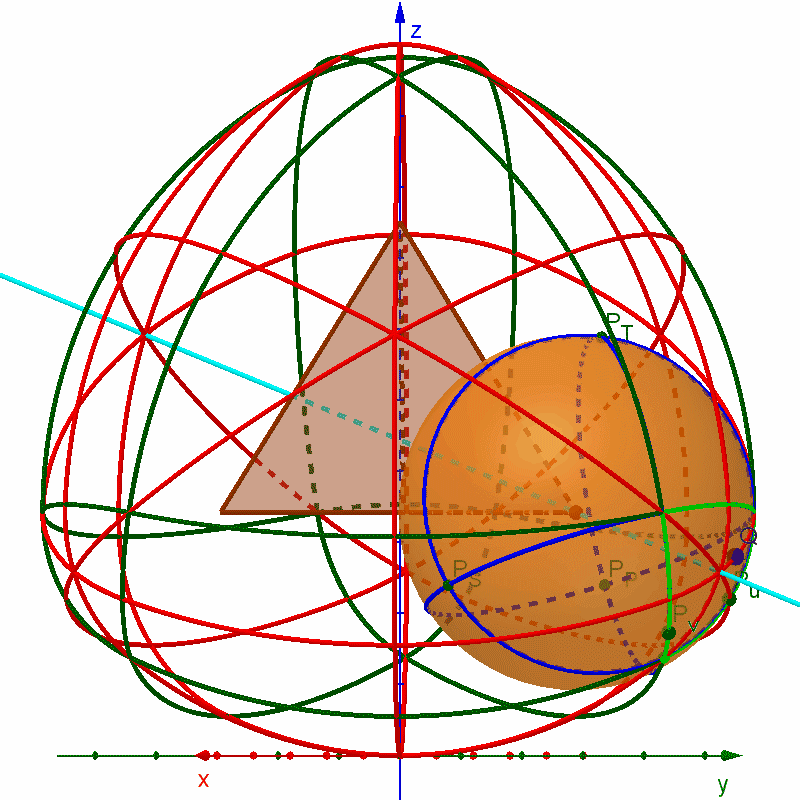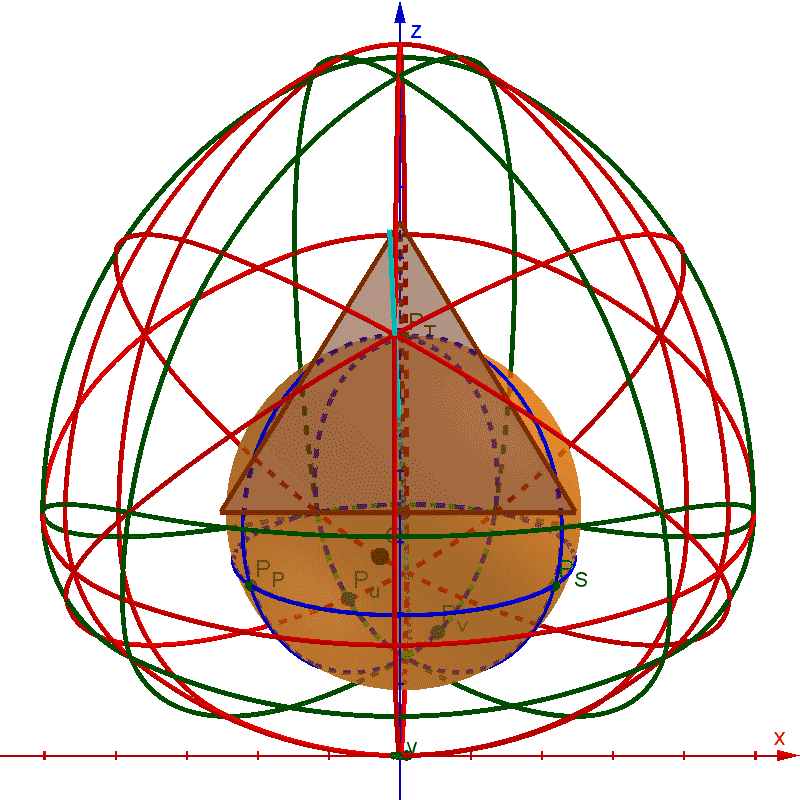
Best Answer
Here's a representation using barycentric coordinates relative to the tetrahedron. Let the vertices of tetrahedron $ABCD$ (of side-length $s$) have these coordinates:
$$ A = s\left(0, 0, \sqrt{\frac23}\right), \quad B = s\left(\frac12, -\frac{1}{2\sqrt3}, 0 \right), \quad C = s\left(-\frac12, -\frac{1}{2\sqrt3}, 0\right), \quad D = s\left(0, \frac1{\sqrt3}, 0\right) $$
We can express a point in space as a weighted average of those vertices: $$P = \frac{\alpha A+\beta B+\gamma C+\delta D}{\alpha+\beta+\gamma+\delta}$$ so that $(\alpha:\beta:\gamma:\delta)$ are the barycentric coordinates of $P$. The barycentric coordinates incorporate the geometry of the tetrahedron in a way the orthogonal Cartesian coordinates don't, offering some benefits especially with respect to symmetrically-arranged elements.
For instance, OP's $P_T$, $P_S$, $P_P$, while defined on an origin-centered sphere (whose radius I'll denote $r$ here), are destined to be translated to a $D$-centered sphere as shown in the rotating figure. The barycentric coordinates of the translated points are a bit nicer —and, importantly, more-nicely related— than their Cartesian counterparts:
$$\begin{align} D+P_T \;&=\; \left(\;(1 + \sqrt2) r \;:\; -r \;:\; -r \;:\; (1 - \sqrt2) r + 2 s \;\right) \\ D+P_S \;&=\; \left(\;-r \;:\; (1 + \sqrt2) r \;:\; -r \;:\; (1 - \sqrt2) r + 2 s \;\right) \qquad \alpha+\beta+\gamma+\delta=2s \\ D+P_P \;&=\; \left(\;-r \;:\; -r \;:\; (1 + \sqrt2) r \;:\; (1 - \sqrt2) r + 2 s \;\right) \end{align}$$
We also find that the translates of $P_u$ and $P_v$ aren't too bad: $$\begin{align} D+P_u \;&=\; \left(\; (1 + \sqrt2 \cot u_+)\,r \;:\; (1 + \sqrt2 \cot u_-)\,r \;:\; -2 \sqrt2 r \sin^2\pi_8 \;:\; -(1 + \mu_u)\,r - \mu_u\, s \;\right) \\ D+P_v \;&=\; \left(\; (1 + \sqrt2 \cot v_+)\, r \;:\; -2 \sqrt2 r \sin^2\pi_8 \;:\; (1 + \sqrt2 \cot v_-)\, r \;:\; -(1 + \mu_v)\,r - \mu_v\, s \;\right) \end{align}$$ where $\alpha+\beta+\gamma+\delta$ is $-\mu_u s$ or $-\mu_v s$, and I'm using a few ad hoc definitions $$ \mu_t := 4 \sin^2\pi_8 + \csc(t_-) \csc(t_+) \qquad t_\pm := \pi_8 \pm t \pi_4 \qquad \pi_n := \pi/n$$
The intervening vectors $n_u$, $n_v$, $d$ are messy, but when the dust settles, I find the barycentric coordinates of the translated point $D+Q$ to be given by $$\begin{align} \alpha &:= r\left(\;\omega + (2 + \sqrt2) \left(-2 (\,\sin(u\pi_2) + \sin(v\pi_2)) + (1 - 2 \sqrt2) \sin((u+v)\pi_2) \right)\;\right) \\ \beta &:= r\left(\; \omega + (2 + \sqrt2) \left(\phantom{-}2 (\cos(u\pi_2) - \sin(v\pi_2)) + \phantom{(1-2\sqrt{2})}\sin((u+v)\pi_2) \right)\;\right)\\ \gamma &:= r\left(\;\omega + (2 + \sqrt2) \left(\phantom{-}2 (\cos(v\pi_2) - \sin(u\pi_2)) + \phantom{(1-2\sqrt{2})}\sin((u+v)\pi_2)\right)\;\right) \\ \delta &:= -(\alpha+\beta+\gamma) + 2 s \left(\begin{array}{c} - 3\sqrt2 + 4 \sin^2\pi_8 \cos((1- 2 u - 2v)\pi_4 ) \\ - 4 \sin\pi_8 \cos((u-v)\pi_4) \cos((1 - 2u - 2v)\pi_8) \\ - 4 \sin(u\pi_4) \sin(v\pi_4) \sin((u+v)\pi_4)) \end{array}\right) \end{align}$$ where $$\omega := 4 \left(\begin{array}{c} \cos^2\pi_8 - \cos(u\pi_4) \cos(v\pi_4) \cos((u+v)\pi_4) \\ + 3 \sin((1- u)\pi_4) \sin((1-v)\pi_4) \sin((u+v)\pi_4) \end{array}\right) $$
Even barring typos, there's likely a simpler way to write all of that. I have a mild suspicion that a "triangular barycentric" parameterization (instead of just $uv$) would exploit the symmetries better, but that's an investigation for another time.
Returning the barycentric coordinates to Cartesian, we use the weighted-average formula with the given coordinates for $A$, $B$, $C$, $D$; the numerous $0$s help out here. In this form, the $D$-translation adds unnecessarily complexity to $y$, so I'll just give the coordinates of $Q$ on the origin-centered sphere: $$\begin{align} Q_x &= -\frac{r}{w}\sqrt3 (2 + \sqrt2)\;(p_+ - q_+) q_- \\[6pt] Q_y &= \phantom{-}\frac{r}{w} \sqrt2\left( 2 + p_- (3 p_+ - 5 q_+) + \sqrt2 p_- (p_+ + q_+) + 2\sqrt2 q_+ (p_+ - 2 q_+)\right) \\[6pt] Q_z &= \phantom{-}\frac{r}{w}\;\left( -1 + \sqrt2 (p_- + 2 q_+) (p_+ + q_+) + 2 q_+ (2 p_- + 3 p_+)\right) \end{align}$$ where $$\begin{align} w &:= \sqrt{3}\left( 1 + 2 \sqrt2 + \sqrt2 (p_- - 2 q_+) (p_+ - q_+) - 2 q_+ (q_+ - 2 p_- )\right) \\ p_\pm &:= \cos \pi_4(u\pm v) \\ q_\pm &:= \sin \pi_4(u\pm v) \end{align}$$
Here, I've opted to express everything in terms of $p_\pm$ and $q_\pm$ to try and keep things notationally uniform, even though trig allows us to combine, for instance, $p_+\pm q_+= \sqrt2 \sin\pi_4(1\pm u\pm v)$.
As with the barycentric representation, I suspect there's an even better way to write all of this. The rampant $\sqrt{2}$s and $\pi_4$s look like they're trying to tell me something. But this is about as far as I can go right now.