Let $X=S^1\vee S^1$ be the wedge sum of two circles. Is there a way to show that $\pi_1(S^1)$ is not isomorphic to $\Bbb Z$, without using the Seifert-van Kampen theorem? (Or is there a way to show that $X$ is not homotopy equivalent to $S^1$?) Since there is a retraction $S^1\vee S^1\to S^1$, and since retraction induces a surjection on $\pi_1$, I see that $\pi_1(X)$ is inifnite. But I can't show $\pi_1(X)$ is not $\Bbb Z$. (I need this to solve an exercise (Hatcher, 1.1.16 (e)) in algebraic topology, but it is in a chapter before Seifert-van Kampen theorem)
Fundamental group of $S^1\vee S^1$ without applying seifert-van kampen’s theorem
algebraic-topologycirclesfundamental-groupshomotopy-theoryretraction
Related Solutions
Question 1: One of the easiest ways to see this 3-fold intersection condition is in terms of "brick subdivisions" of the square. This is a subdivision of the square into rectangles such that each vertex of the subdivision is a corner of 3-rectangles. Such a subdivision can be taken fine enough to carry out the argument given in Hatcher's book. More details are in
R. Brown and A. Razak Salleh, ``A van Kampen theorem for unions of non-connected spaces'', Archiv. Math. 42 (1984) 85-88.
which relates this argument to the Lebesgue covering dimension. Also by using the fundamental groupoid $\pi_1(X,A)$ on a set $A$ of base points, it gives a theorem for the union of non-connected spaces.
I also prefer the argument in terms of "verifying the universal property" rather than looking at relations defining the kernel of a morphism. To see this proof in the case of the union of 2 sets, see
https://groupoids.org.uk/pdffiles/vKT-proof.pdf
One of the problems in the proof for the fundamental group as given by May is that it does not generalise to higher dimensions.
Question 2: One has to ask: where do such unions of non-connected spaces arise? The standard answer, and for me from which all this groupoid work arose, is to obtain the fundamental group of the circle $S^1$, which is after all, THE basic example in algebraic topology. Many other examples arise in geometric topology.
More answers come in applications to group theory; for example the Kurosh subgroup theorem on subgroups of free products of groups can be proved by using a covering space of a one-point union of spaces. The cover over each space of this union has usually many components. I confess I have not seen the minimal condition of 3-fold intersection used in practice, but it is always interesting to know the minimal conditions for a theorem. Just as well to know one can't in general get away with 2-fold intersections.
You can see the consistent use of groupoids in $1$-dimensional homotopy theory (van Kampen theorem, homotopy theory, covering spaces, orbit spaces) in my book Topology and Groupoids (2006) available from amazon.
Edit Feb 17, 2014:
It may be useful to point out that a sharper result than that in May's book was published in 1984 in the above Brown-Razak Salleh paper; the idea of proving a pushout result for the full fundamental groupoid, and then retracting to $\pi_1(X,A)$, is in my 1967 paper, and subsequent book, but Peter May cleverly makes it work for infinite covers; the problem is that this proof does not generalise to higher dimensions, as far as I can see.
Also Munkres' book on "Topology" uses non path connected spaces in dealing with the Jordan Curve Theorem, and for this uses covering space rather than groupoid arguments. I do not see why books avoid $\pi_1(X,A)$, since it hardly requires any extra in the proofs to that for $\pi_1(X,a)$, given the easy definition.
Edit Feb 20, 2015: A relevant question and answer is https://mathoverflow.net/questions/40945/compelling-evidence-that-two-basepoints-are-better-than-one
Some of the relevance to the history of algebraic topology, and to further developments, is in this presentation in Galway, December, 2014. See also my preprint page.
March 5, 2015
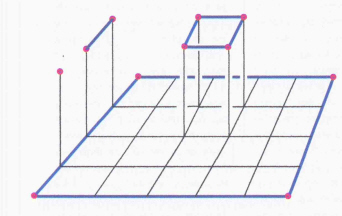
I feel this "perturbation (or deformation) trick" is of quite a fundamental nature. Above is a picture of part of a deformation involved in the proof of the 2-dimensional Seifert-van Kampen type theorem, for the crossed module involving a triple $(X,A,C)$ of spaces where $C$ is a set of base points, and $C \subseteq A \subseteq X$.
The red dots denote points of $C$. The blue lines denote paths lying in $A$. The small squares in the bottom are supposed to denote squares lying in a set $U$ of an open cover. By making connectivity assumptions you can deform a small bottom square into the top one of the right kind, and still lying in the same open set. So, by working with a double groupoid construction $\rho_2(X,A,C)$ whose compositions are more 2-directional than the usual relative homotopy groups, you can get going with the proof of a universal property involving double groupoids, and hence for crossed modules.
We use the Seifert Van-Kampen Theorem to calculate the fundamental group of a connected graph. This is Hatcher Problem 1.2.5:
It is a fact in graph theory that any connected graph $X$ contains a maximal tree $M$, namely a contractible graph that contains all the vertices of $X$. Now if the maximal tree $M = X$, then we are done because for any $x_0 \in M$, $\pi_1(M,x_0) = \pi_1(X,x_0) = 0$ that is trivially free. Now suppose $M \neq X$. Then there is an edge $e_i$ of $X$ not in $M$. Observe that for each edge $e_i$ we get a loop going in $M \cup e_i$ about some point $x_0 \in M$. Now fix out basepoint $x_0$ to be in $M$ and suppose that the edges not in $M$ are $e_1,\ldots,e_n$. Then it is clear that $$X = \bigcup_{i=1}^n \left(M \cup e_i\right).$$
The intersection of any two $M \cup e_i$ and $M \cup e_j$ contains at least $M$ and is path connected, so is the triple intersection of any 3 of these guys by the assumption that $X$ is a connected graph. So for any $x_0 \in M$, the Seifert-Van Kampen Theorem now tells us that
$$\pi_1(X,x_0) \cong \pi_1(M \cup e_1,x_0) \ast \ldots \ast \pi_1(M \cup e_n,x_0)/N$$
where $N$ is the subgroup generated by words of the form $l_{ij}(w)l_{ji}(w)^{-1}$, where $l_{ij}$ is the inclusion map from $\pi_1((M\cup e_i) \cap (M \cup e_j),x_0) = \pi_1(M \cup (e_i \cap e_j),x_0)$. Now observe that if $i \neq j$ then $M \cup (e_i \cap e_j) = M$ and since $\pi_1(M,x_0) = 0$ we conclude that any loop $w \in \pi_1(M \cup (e_i \cap e_j),x_0)$ in here is trivial. If $i = j$, $l_{ij}$ is just the identity so that our generators for $N$ are just
$$l_{ij}(w)l_{ji}(w)^{-1} = ww^{-1} = 1$$
completing our claim that $N$ was trivial. Now for each $i$, we have that $\pi_1(M\cup e_i,x_0)$ is generated by a loop that starts at $x_0$ and goes around the bounded complementary region formed by $M$ and $e_i$ and back to $x_0$ through the maximal tree. Such a path back to $M$ does not go through any other edge $e_j$ for $j$ different from $i$. It follows that $\pi_1(X,x_0)$ is a free group with basis elements consisting of loops about $x_0 \in M$ as described in the line before.
Best Answer
There are two retractions $p_1, p_2 : S^1 \vee S^1 \to S^1$ which induce two different surjections $\pi_1(S^1 \vee S^1) \to \pi_1(S^1) \cong \mathbb{Z}$, and in fact together they give a map $S^1 \vee S^1 \to S^1 \times S^1$ which induces a surjection on $\pi_1$ (you can show this very explicitly by just lifting a pair of loops to a loop). So $\pi_1(S^1 \vee S^1)$ admits a surjection onto $\mathbb{Z}^2$ and hence can't be $\mathbb{Z}$.
Exercise 1.1.16(e) in Hatcher asks you to show that a disk with two boundary points identified $D$ doesn't retract onto its boundary $S^1 \vee S^1$. You can do this more directly than the above, by just showing that the induced map $\pi_1(S^1 \vee S^1) \to \pi_1(D) \cong \mathbb{Z}$ isn't injective. And this is pretty straightforward: the two loops in $S^1 \vee S^1$ map to the same element of $\pi_1(D)$ but they can be distinguished by either of the retractions $p_1, p_2$. (This doesn't even require that you be able to calculate $\pi_1(D)$.)
Without Seifert-van Kampen but with some other tools more options are available if you just want to show that $\pi_1(S^1 \vee S^1)$ can't be $\mathbb{Z}$. If homology is available you can compute that $H_1(S^1 \vee S^1) \cong \mathbb{Z}^2$. And if covering spaces are available it suffices to exhibit a Galois cover with non-cyclic Galois group, or show that there are non-isomorphic covers of the same degree, and it's easy to write these down explicitly. In fact you can classify the covering spaces by hand in a way that will prove that the fundamental group is $F_2$ without Seifert-van Kampen, e.g. by writing down the universal cover as the Cayley graph of $F_2$.