The boundary of a Möbius band is an unknot in $\mathbb{R}^3$, so we can deform it via an ambient isotopy to the standard circle in a plane. In this way, how does the Möbius band look like (i.e. how the standard circle bounds a Möbius band in $\mathbb{R}^3$)? I can hardly imagine it. Could someone visualize it?
Deform the boundary of the Möbius band in the proper way
differential-topologygeneral-topologygeometric-topologymobius-bandvisualization
Related Solutions
The Mayer-Vietoris sequence is defined as the long exact sequence
$$H_*(U \cap V) \to H_*(U) \oplus H_*(V) \to H_*(X)$$
where the first map is defined by $(i_*, j_*)$ and the second map is defined by $k_* - l_*$ where $i, j$ are the inclusion maps of $U \cap V$ inside $U$ and $V$ and $k, l$ are the inclusions of $U$ and $V$ inside $X$.
If $X$ is the Klein bottle, $\{U, V\}$ cover of it by the two mobius strips, then $U \cap V$ is homotopy equivalent to the boundary of the two strips. I have to thus compute the maps $i_*, j_*$ induced on homology where $i, j$ are inclusions of the boundary map of the mobius strips into the Klein bottle.
That's precisely where we need the wrapping description. If $M$ is a moebius strip then the inclusion map $\partial M \hookrightarrow M$ could be understood as follows: deformation retract $M$ to it's core circle, which generates $H_1(M)$. Under this deformation retract $\partial M$ maps to twice the core circle. So $i_* : H_1(\partial M) \to H_1(M)$ is precisely the multiplication by $2$ map.
Thus, $i_*$ is multiplication by $2$ whereas $j_*$ is multiplication by $-2$ due to orientation issues. Tat tells you $\alpha$ sends $1$ to $(-2, 2)$ once you identify $H_1(U \cap V)$ with $\Bbb Z$ and $H_1(U) \oplus H_1(V)$ with $\Bbb Z \oplus \Bbb Z$.
Topologically the full-twist strip and the untwisted strip are identical. The only difference is the way they are immersed in $\Bbb R^3$. So you aren't going to get an intrinsic characterization that is like the quotient space one you mentioned. (To see this, consider how you make a full-twist strip: take the untwisted strip, cut it across, twist it, and then rejoin each point on the cut to exactly the same points it was attached to before the cut. Or imagine twisting the strip in $\Bbb R^4$ instead of in $\Bbb R^3$.)
Knot theory faces a similar problem. Two linked circles are topologically identical to two unlinked circles: they are both the disjoint union of two circles. (Compare these with the boundaries of your two kinds of strips.) But knot theory wants to distinguish not the spaces themselves but the way they are immersed in $\Bbb R^3$. One way this is done is to consider the complement of the two sets in $\Bbb R^3$. Say the full-twist strip is $F_2$ and the no-twist strip is $F_0$. Then consider the spaces $ \Bbb R^3-F_2$ and $\Bbb R^3-F_0$. These are topologically distinct. But to really carry this out may be difficult.
Best Answer
Werner Boy's Surface (with a Hole)
A really nice way to represent it is Boy's Surface with a hole poked in it.
Boy's surface is an immersion of the 2-dimensional projective plane $P$ into Euclidean $\Bbb R^3$. It's not an embedding because it has self-intersections and a triple point. But it's smooth everywhere and has no pinches or creases or cusps.
Now $P=M+D$ where $M$ is a Möbius band and $D$ is a disk, i.e. gluing $D$ and $M$ together gives $P$. The other way round, poking a hole (removing $D$) from $P$ will yield $M$. Notice that we can pick to remove a disc that does not intersect with the remaining $M$.
The page above has images of a sculpture in Oberwolfach, which is specially nice because it is minimizing Willmore energy using Bryant-Kusner-parametrization. Removing the top dome would leave a Möbius band with a flat circle as its boundary.
And there are also nice animations, cf. youtube: Boy's surface.
Great David Hilbert conjectured that no such immersion exists, but Werner Boy proved him wrong.
Möbius Snail
A different representation with circular boundary is the "Sudanese Möbius strip" which has no self-intersections. An image and description are here.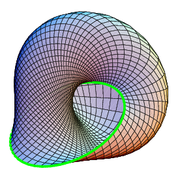
Adding a disc in order to complete it to the projective plane will introduce self-intersections and creases, though, i.e. places where the surface is not smooth. More renderings are here.
Möbius Wheel (from Boy's Surface)
Returning to Boy's surface, here are some renderings of a Möbius strip with (almost) circular boundary: W1, W2, W3, W4. These renderings were created by changing the Bryant-Kusner parametrization in such a way that only a part is rendered (which effectively pokes a hole) and by pulling the boundary of the resulting Möbius strip to the equatorial plane. The resulting shape has $D_{2\cdot 3}$ dihedral symmetry with a triple-point in the center. There is a detailed description.
All images from Wikipedia / Wikimedia Commons.